СТРОИТЕЛЬНАЯ МЕХАНИКА И РАСЧЕТ СООРУЖЕНИЙ   ISSN 0039-2383             №3  2019,  с.31-38

УДК 624.044

К ВОПРОСУ ОБ ОПРЕДЕЛЕНИИ РАСЧЕТНЫХ ДЛИН СТЕРЖНЕВЫХ ЭЛЕМЕНТОВ РАМНЫХ ПРОСТРАНСТВЕННЫХ СИСТЕМ

Е.И.Бритвин, канд. физ.-мат. наук

 

Построен эффективный вычислительный алгоритм, позволяющий находить расчетные длины стержневых элементов рамных конструкций. Для каждого элемента формируется матрица реакций со стороны отбрасываемой части системы и, с учетом этих реакций, решается задача о собственных значениях уравнения продольного изгиба стержня. При поиске собственных значений напряженное состояние системы фиксируется. Решение точное. Продемонстрировано высокое быстродействие алгоритма.

Проверка локальной устойчивости стержневых элементов является одной из важнейших проверок, необходимых для обеспечения надежной работы строительных конструкции. Без этой проверки не обходится практически ни один расчет. В то же время, каждый расчетчик знает, сколько неопределенности таит в себе эта проверка. Проблема связана с тем, что для ее выполнения для каждого стержня проверщик должен задаться так называемой “расчетной длиной”. Как правило, программные комплексы способны выдать этот параметр (расчетная длина является побочным продуктом проверки общей устойчивости конструкции). Но очень часто вычисленные значения оказываются за пределами разумного. В частности, для слабо нагруженных стержней программа может выдать огромные величины, не укладывающиеся ни в какие естественные представления о природе данной проверки. Аналогичная ситуация происходит, если в конструкцию “затесался” какой-нибудь слабый стержень, теряющий устойчивость значительно раньше, чем вся конструкция (вырожденная форма потери устойчивости). В этом случае программа вычисляет параметры устойчивости всех остальных стержней, ориентируясь на это найденное заниженное критическое значение, выдавая полный абсурд. Практика показывает, что вычисленными программой значениями расчетных длин реально можно воспользоваться не более, чем для 5-10% стержневых элементов, входящих в конструкцию. Для остальных элементов расчетчик должен обращаться к различным справочникам и нормам [3]-[6], которые далеко не всегда охватывают все возможные случаи. Некоторые авторы предлагают полуаналитические решения, выделяя ограниченный фрагмент конструкции, примыкающий к тестируемому стержню [1], [2]. К сожалению, разобраться в данной ситуации, понять, когда можно воспользоваться данными, предоставляемыми расчетом, или следует обращаться к справочникам, может только очень опытный проектировщик. Поэтому проверка локальной устойчивости стержневых элементов часто напоминает гадание на кофейной гуще.

Для преодоления данной проблемы, авторами в свое время был разработан специальный алгоритм [7], позволяющий оценить работоспособность конструкции не используя понятия “расчетной длины стержня”. Причина преждевременной (по сравнению с теорией Эйлера) потери устойчивости стержневых элементов состоит в наличии в стержнях малых, незаметных глазу, начальных несовершенств (проще говоря, малых начальных искривлений). Поэтому, даже при центральном сжатии такого стержня, в нем возникает моментное напряженное состояние. Если с увеличением нагрузки суммарное напряжение от сжатия и изгиба в одном из фибровых волокон стержня достигает предела текучести, то в теле стержня возникают необратимые изменения и стержень теряет устойчивость (потеря устойчивости второго рода). Основываясь на физической модели этого явления, был разработан специальный конечный элемент стержня с начальной погибью в форме параболы. Предельные значения глубин неровностей нормировались соответствующим СП. Учитывая, что глубина неровности – это случайная величина, алгоритм выполнял серию расчетов по деформированной схеме, генерируя случайным образом знаки и значения амплитуд неровностей. Предполагалось, что глубины неровностей распределены по нормальному закону в интервале [0,X], где X – предельное значение глубины начальной неровности. Центр распределения принимался в точке X/2. Стандарт распределения принимался равным X/5 (величина стандарта X/5 была выбрана произвольно – исследования показали, что результат мало зависел от величины стандарта). В результате, по сформированным выборкам, для каждого стержня алгоритм вычислял математическое ожидание и стандарт отклонения фибровых напряжений. На основе этих данных путем статистической обработки для каждого стержня определялось предельное фибровое напряжение сжатия, которое гарантированно не будет превышено с заданной вероятностью. Сравнивая это напряжение с R_y, делался вывод о несущей способности стержня. Алгоритм был успешно реализован на программном комплексе Selena[8].

Поскольку наши отечественные СП не предусматривают такой тип проверки (заметим, в Eurocode 3 [5] есть прямое разрешение проверки с учетом начальных несовершенств), несмотря на существенное облегчение, пользователи программы все равно, в заключение, вынуждены были подкреплять расчет стандартной проверкой локальной устойчивости стержневых элементов по методике СП. Обычно путь решения был таков – пользователи вначале подбирали нужные сечения, основываясь на расчете по программе (программа в очень наглядной форме позволяет выявить все слабые элементы), а затем, со значительно меньшим риском “промахнуться” в выборе расчетных длин, выполнялась стандартная проверка. Но даже в этой ситуации, необходимость задаваться расчетными длинами, которые чаще всего, неизвестно откуда брать, связано с большим объемом ручной работы и значительными психологическими неудобствами.

Целью данной работы является разобраться, по возможности, в том, что же все-таки такое “расчетные длины” и, возможно, дать рекомендации по их определению. Физически расчетная длина стержня – это расстояние между парой соседних нулей на эпюре моментов стержня, подверженному продольному изгибу. Этим, считается, произвольный стержень как бы приводится к шарнирному с обоих концов стержню, для которого решение задачи продольного изгиба хорошо известно. Среди специалистов, однако, существует мнение, что методика проверки устойчивости стержневых элементов на основе расчетных длин вообще не имеет четкого научного обоснования. На самом деле, это не совсем так. Можно показать, что методика проверки произвольного стержня, подвергнутого продольному изгибу, может быть выполнена по тем же формулам, что и шарнирно оперный стержень. Автору, к сожалению, не удалось найти в литературе этого доказательства (хотя есть большие подозрения, что оно где-то все же существует). Поэтому мы приведем здесь этот коротенький вывод, тем более, что его результат очень важен для нашего дальнейшего изложения.

На рис.1 показан стержень с начальной погибью, заданной функцией f(x). На стержень действует продольная сжимающая сила N. В результате деформации стержень приобретает дополнительное перемещение y(x). Реакции отброшенной части конструкции условно показаны жирными пунктирными линиями.

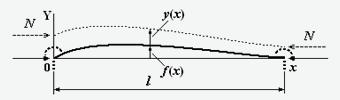
Рис.1

Уравнение продольного изгиба балки, с начальной погибью f(x) имеет вид (рис.1)

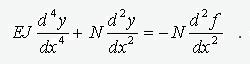
Пусть начальная погибь описывается выражением вида

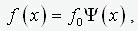
где f₀ – “глубина” погиби, а Y(x) – некоторая, определенным образом нормированная функция. Примем в первом приближении, что функция Y(x) совпадает с решением однородного дифференциального уравнения вида (1) при соответствующих граничных условиях. Т.е. Y(x) удовлетворяет уравнению

,

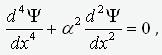
где a – собственное значение краевой задачи. Решением этого уравнения является выражение вида

.

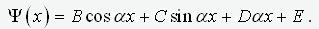
Не ограничивая общности, пронормируем это выражение так, чтобы выполнялось условие B²+C²=1. Очевидно, выражение

,

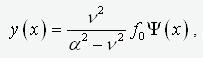
является решением уравнения (1), где n²=N/EJ. В этом нетрудно убедиться, подставив (5) в уравнение (1). При этом решение y(x), по определению функции Y(x), будет удовлетворять заданным граничным условиям. Т.е., то, что требуется.

Выразим изгибающий момент в балке по формуле 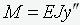. Учитывая выражение (4), получаем

.

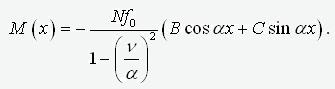
Поскольку расчетная длина стержня l_p– это расстояние между нулями эпюры момента, из выражения (6) немедленно следует – al_p=p. А экстремум этого выражения достигается в точке x₀, удовлетворяющей условию cos(ax₀)=B и sin(ax₀)=C. В результате, получаем

.

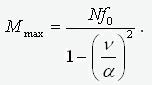Таким образом, уточняется физический смысл “глубины” f₀ – это амплитуда неровности над линейной компонентой. Вычислим фибровое напряжение в точке, где момент достигает максимума

.

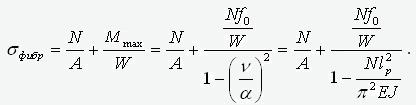где A, J и W – площадь, момент инерции и момент сопротивления сечения. Преобразуем это выражение следующим образом

.

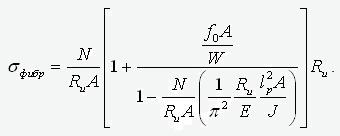Учитывая, что J/A=i² - радиус инерции сечения и l_p/i=l - гибкость стержня, а также вводя обозначения 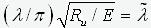- приведенная гибкость, 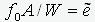- приведенный эксцентриситет и N/R_uA=j, получаем

.

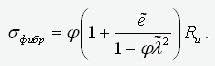
Определим теперь, при каком условии фибровое напряжение достигает предела текучести, т.е. 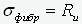. В результате уравнение (7) приобретает вид

.

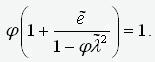Избавляясь в этом выражении от знаменателя, приходим к квадратному уравнению

.

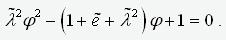Его решение

,

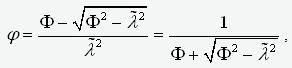
где .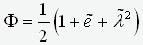

Таким образом, посредством небольшого обобщения нам удалось показать, что формула (8), которая, обычно, выводится для шарнирно опертого стержня, применима без изменений и к общему случаю закрепления концов стержня. Данный вывод, конечно, нельзя считать строгим. Во-первых, мы ограничились формой неровности, и вопрос о выборе наихудшей формы остался открытым (хотя интуиция подсказывает, что в нашем выборе есть рациональное зерно). Во-вторых, находя максимум момента, мы не исследовали значения на границе интервала. Но выбор в качестве максимума выражения (6) точки экстремума, гарантирует нам, что максимальное значение момента на отрезке [0,l] будет, по крайней мере, не больше выбранного значения.

Данное исследование имеет еще один недостаток. Несмотря на то, что неровность входит в уравнение (1) через вторую производную и, казалось, это дает возможность варьировать линейными членами в выражении (4), решение можно считать справедливым, только если форма начальной неровности строго пропорциональна собственной форме потери устойчивости стержня. Потому что только в этом случае решение (4), (5) будет строго удовлетворять граничным условиям задачи. С другой стороны, под неровностью мы привыкли понимать отклонение от линии, соединяющей точки крепления стержня. Это значит, что в начале и конце стержня эта функция должна быть равна нулю, что отнюдь не всегда является непременным атрибутом формы потери устойчивости. Таким, “придавленным” к концам стержня эквивалентом выражения (4), является выражение

,

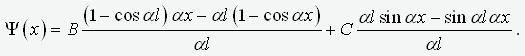
На рис.2 показаны эпюры моментов консольного стержня, сжатого одной и той же силой, равной половине критической при различных формах начальной неровности: a). по форме потери устойчивости - 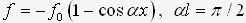; b). по параболе - 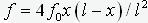; c). по “прижатой” форме потери устойчивости - 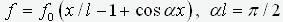. Для всех трех случаев нормирующий коэффициент был принят равным f₀=0.01. Параметры стержня – l=2, EJ=1.

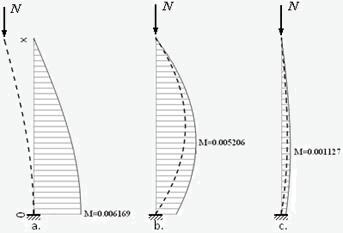
Рис.2

Пунктирными линиями показана форма неровности в утрированном масштабе. Эпюры моментов определены выражениями

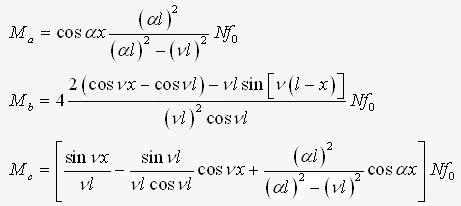
где al=p/2, n²=N/EJ. Рядом с эпюрами показаны максимальные значения момента. Как видно, наибольшее значение момента получилось для варианта а. – неровность, пропорциональная форме потери устойчивости. Заметим, именно эта форма неровности заложена в приведенный выше вывод, конечным результатом которого является формула (8). В рамках данного исследования было проделано еще несколько численных экспериментов на простых рамах. В связи с ограниченностью места мы не приводим этих результатов. Но во всех случаях неровность, пропорциональная форме потери устойчивости, при прочих равных условиях давала наибольший максимальный момент. Данное исследование, конечно, нельзя рассматривать как доказательство того, что неровность в виде формы потери устойчивости стержня всегда будет приводить к наибольшему моменту. Но можно сделать допущение (praesumptio), что в большинстве случаев это будет именно так (тем более, что при приближении усилия к критическому значению вид кривой деформации неизбежно будет стремиться к форме потери устойчивости).

Из вышеизложенного следует – чтобы определить значение продольного усилия в отдельном стержне, при котором в одной из его фибр возникнет напряжение, равное пределу текучести, надо: 1) решить для этого стержня задачу о собственных значениях уравнения (3); 2) по формуле l_p=p/a вычислить расчетную длину стержня (a – собственное значение); 3) от расчетной длины l_p перейти к гибкости l и по формуле (8) вычислить коэффициент устойчивости j; 4) определить искомое предельное значение усилия N=jR_uA (точнее, его нижнюю границу). Самое сложное в данном перечне – это, конечно, решить краевую задачу для уравнения (3). Задача осложнена тем, что условия на концах тестируемого стержня обеспечиваются реакциями в узлах крепления стержня со стороны остальной части конструкции. Иными словами, мы должны уметь вычислить матрицу реакций от единичных смещений связей, наложенных на пару узлов, к которым крепится наш стержень. Причем, чтобы иметь возможность варьировать значением усилия в самом тестируемом стержне, мы должны из конструкции предварительно исключить сам этот стержень.

Стандартная процедура нахождения расчетных длин стержневых элементов состоит из двух этапов – вначале вычисляются продольные усилия в стержнях от заданной комбинации загружений, затем вводится единый для всех найденных усилий множитель и отыскивается его критическое значение, при котором система теряет устойчивость. По найденным значениям усилий N_кр,i, соответствующих критическому состоянию, по формуле 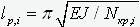вычисляются расчетные длины стержней. Очевидно, этот процесс полностью эквивалентен описанной выше процедуре, с той разницей, что при решении задачи о собственных значениях уравнения (3) вместе с изменением усилия в тестируемом стержне, пропорционально меняются и усилия в отброшенной части системы. Такое параллельное “необоснованное” увеличение усилий во всех элементах конструкции приводит к тому, что реакция отброшенной части на стержень падает, делая стержень более слабым и, как следствие, мы получаем завышенные расчетные длины и, соответственно, заниженную несущую способность стержня. Описанный же выше алгоритм предлагает фиксировать усилия в отброшенной части системы, а варьировать только усилием в тестируемом стержне. Неоспоримым достоинством “стандартного” алгоритма является то, что все расчетные длины вычисляются в результате одной процедуры, хотя это вряд ли может служить оправданием его малой эффективности. В то же время, предлагаемый вариант требует дифференцированного подхода к каждому стержню. С другой стороны, то, что решение задачи устойчивости всей системы распадается на ряд мелких задач (не более 12 переменных – 2 узла по 6 степеней свободы) позволяет построить эффективные алгоритмы решения данной проблемы.

На рис.3b. показан график зависимости расчетной длины ригеля рамы, изображенной на рис.3а. (жесткости стоек и ригеля одинаковые), от усилий в стойках N₁ и N₂. Шкалы N₁ и N₂ проградуированы в долях от критического значения соответствующих усилий. Как видно, расчетная длина ригеля практически не зависит от значений усилий в стойках вплоть до 80% запаса конструкции по устойчивости. После достижения усилиями этой границы начинается резкий рост расчетной длины вплоть до бесконечности. На рис.2c. показан график зависимости расчетной длины левой стойки рамы. На этом рисунке можно проследить отличие “стандартной” и предлагаемой методик. Если, например, усилия в колоннах определены положением точки А, соответствующей 40% (левая колонна более нагружена – N₁:N₂=10:4) от критической нагрузки, то расчетная длина левой стойки составляет 1.7445м. По “стандартной” методике получаем l_p=1.9372м (выход по лучу 0-А на “общую потерю устойчивости”). Аналогично, для точки В, также соответствующей 40% от критической нагрузки (N₁:N₂=2:10) получаем l_p=2.0022м и l_p=4.0172м. Как видно, во втором случае рост параметра l_p с выходом на границу общей потери устойчивости значительно больше. Это, как раз и есть проявление общей болезни “стандартной” методики – чем менее нагружен элемент, тем больше его расчетная длина. Для ригеля выход на границу общей потери устойчивости вообще эквивалентен катастрофе – значение l_p стремится к бесконечности. Это происходит по причине того, что усилие в нем равно нулю. В то же время, в подавляющей части области определения параметров N₁ и N₂ расчетная длина ригеля имеет вполне разумное и почти постоянное значение.

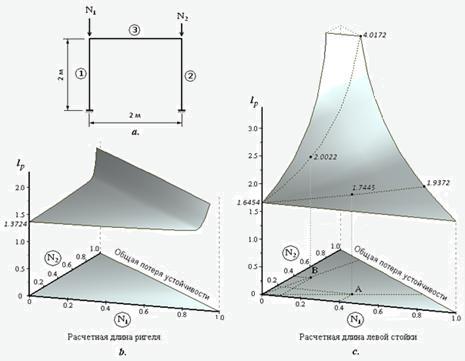
Рис.3

На рис.4 показана расчетная схема 4-х-этажной 4-х-пролетной рамы. Все стержни одинакового сечения. Этажи и перекрытие загружены одной и той же распределенной нагрузкой.

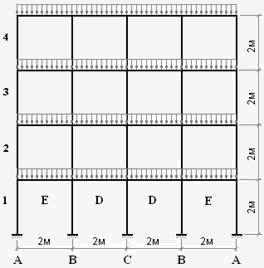
Рис.4

На графиках рис.5 показаны рассчитанные кривые коэффициента свободной длины m для колонн (A,B,C) и ригелей (D,E). На этих графиках по шкале абсцисс откладывается уровень нагрузки по отношению к критическому состоянию. Цифрами обозначены номера этажей.

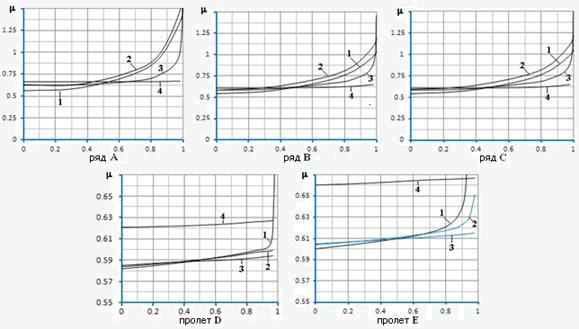
Рис.5

В таблице 1 даны предельные значения коэффициента m, соответствующие критическому состоянию конструкции. Заметим, эти предельные значения как раз и соответствуют “стандартной” схеме расчета, когда при поиске критического состояния увеличение нагрузки происходит одновременно во всех элементах системы. Как следствие, в элементах ригелей, в которых изначально не было никаких усилий, получилось значение m=∞ (эффект огромных расчетных длин для слабо нагруженных элементов расчетчикам хорошо известен).

Таблица 1

 

На рис.6a изображена шпренгельная ферма, подкрепленная в пяти точках верхнего пояса из своей плоскости. Верхний пояс составлен из двутавров СТО АС4М 20-93 16В2 (J_y=6.83∙10^-7, J_z=8.69∙10^-6). Нижний пояс – двутавр 12В2 (J_y=2.77∙10^-7, J_z=3.18∙10^-6). Раскосы и стойки – квадратный профиль 60х6. Шпренгельные связи – квадрат 50х5.5. К верхнему поясу приложена вертикальная распределенная нагрузка 15000 Н/м, что составляет 92% от критической нагрузки (потеря устойчивости происходит выпучиванием из плоскости фермы).

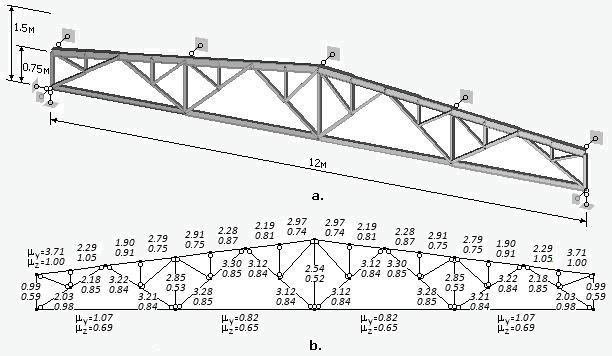
Рис.6

На рис.6b рядом с каждым элементом фермы показаны рассчитанные значения коэффициента свободной длины m: верхние значения соответствуют изгибу элементов из плоскости фермы, нижние – в плоскости фермы. На рис.7 даны значения коэффициента свободной длины для элементов той же фермы, рассчитанные по “стандартной” методике.

Рис.7

Стандартная методика позволяет вычислить расчетные длины только для сжатых элементов и только при изгибе относительно одной из главных осей стержня (в данном случае, при изгибе из плоскости фермы). Как видно, есть некоторое соответствие между значениями коэффициента m_y для элементов верхнего пояса между точками крепления опорных раскосов, рассчитанным по обеим методикам. Все остальные элементы слабо нагружены и для них программа выдает неприемлемые значения коэффициента m.

Описанный выше алгоритм был успешно реализован на базе программного комплекса Selena [8]. Алгоритм последовательно для каждого стержня строит матрицу жесткости отброшенной части системы в узлах крепления стержня и затем решает для тестируемого стержня задачу о собственных значениях при найденных силовых граничных условиях. Алгоритм показал свою чрезвычайную эффективность. Благодаря тому, что задача о собственных значениях распадается на множество мелких задач, алгоритм работает очень быстро. Так расчет пространственной рамной системы 10х10 пролетов и 10 этажей (1331 узел, 3410 стержней, ширина ленты после перенумерации 97 узлов) на компьютере DELL 6400 (процессор Intel Core 2 Duo T9550, 2.66GHz) время решения задачи составило 14.4 сек. (статика – 5.7 сек.). Важно отметить, что в рамках предложенного подхода не существует проблемы “огромных расчетных длин”. Расчетные длины могут быть вычислены независимо друг от друга для обеих главных осей сечения. Понятие “расчетная длина” совершенно естественным образом может быть распространено на ненагруженные, и даже растягиваемые элементы. И, наверно, самое главное, формальный подход к решению данной проблемы позволяет практически полностью автоматизировать процедуру проверки локальной устойчивости стержневых сечений.

Литература

1. Oppe M., Muller C.,Iles C., NCC: buckling length of columns; rigorous approach, London, Accsess Steel, 2005.

2. Webber A., Orr J.J., Shepherd P., Crothers K., The effective length of columns in multi-storey frames, Engineering Structures, 102 (2015),132-143.

3. СП 16.13330.2011, Стальные конструкции, СНиП II-23-81*, Москва, 2011.

4. AISC. AISC manual of steel construction. Load and resistance factor design. Chicago, AISC,2001.

5. Eurocode 3: Design of steel structures –Part 1-1: General rules and rules for buildings, EN 1993-1-1,2005.

6. Лейтес С.Д. Справочник по определению свободных длин элементов стальных конструкций, М.: Проектстальконструкция, 1967.

7. Бритвин Е.И., Тарнопольский А.А., К вопросу о проверке устойчивости стержневых конструкций, ж. Будiвницьтво Украiни, №1, 2006г. с.22-27.

8. Прочность, устойчивость, колебания. Универсальный программный комплекс для расчета конструкций на прочность SELENA. Сайт selenasys.com, -389 C.