СТРОИТЕЛЬНАЯ МЕХАНИКА И РАСЧЕТ СООРУЖЕНИЙ   ISSN 0039-2383               №4  2016,  с.43-54

УДК 624.044

К РАСЧЕТУ РАМНЫХ КОНСТРУКЦИЙ СОСТАВЛЕННЫХ ИЗ ТОНКОСТЕННЫХ СТЕРЖНЕВЫХ ЭЛЕМЕНТОВ

Е.И.Бритвин, канд. физ.-мат. наук

Теория деформации тонкостенных стержней, берущая начало от работ Власова [1], прекрасно подтверждена на множестве численных экспериментах на конечноэлементных моделях. Однако применение ее к расчету рамных конструкций сопряжено с рядом серьезных трудностей. Естественный путь решения этой проблемы состоит в добавлении к шести стандартным перемещениям узла (три перемещения и три поворота) седьмой компоненты – депланации и построении на базе такой семикомпонентной модели матрицы жесткости стержня. Но при этом неизбежно следует ответить на вопрос, – каким образом можно свести депланации отдельных стержней, подходящих к узлу, к одному показателю. Наиболее просто эта проблема решается, если конструкция представляет собой неразрезную балку постоянного сечения. В этом случае, очевидно, депланации подходящих к узлу с обеих сторон сечений равны. Однако, если узел имеет более сложную конструкцию, ответ не столь очевиден. Из-за неоднозначности ответа на этот вопрос некоторые авторы ограничиваются или свободным присоединением стержня к узлу (шарнир относительно депланации) или полным защемлением подходящего к узлу сечения [2,4]. Некоторые авторы предлагают моделировать узлы плоскими конечными элементами и к ним присоединять стержневые элементы с 7-ю степенями свободы в узле [7]. Наиболее простое решение, конечно, состоит в предположении, что депланация передается через узел непрерывно [6]. У этой гипотезы есть как сторонники, так и противники. Так, в работе [3] и некоторых других работах высказываются большие сомнения по этому поводу. В настоящей работе еще раз проверяется несостоятельность гипотезы равенства депланаций подходящих к узлу элементов и предлагается метод формирования матрицы жесткости узла, позволяющий учесть несовпадение депланаций подходящих к узлу сечений.

Проверку можно осуществить на конечноэлементных моделях узлов. Для этого нам надо уметь вычислять депланацию сечений конечноэлементных моделей стержней по их деформациям. Продольные перемещение точек тонкостенного сечения описывается выражением 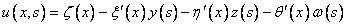[1]

,                                           (1)

где x – координата вдоль оси стержня, s – координата вдоль дуги сечения, ζ(x), ξ(x), η(x) - перемещения точек, расположенных на оси, проходящей через центр изгиба сечения, θ’(x) - депланация сечения, y(s) и z(s) – декартовы координаты точки сечения в главной системе координат, w(s) – секториальная координата точки сечения. Таким образом, задача состоит в том, чтобы по известным перемещениям точек сечения u(x,s) восстановить параметры ζ(x), ξ’(x), η’(x) и  θ’(x). В работе [3] для нахождения искомых параметров на основе выражения (1) строится невязка между экспериментальными и теоретическими значениями продольного перемещения и находится минимум суммы квадратов невязок по искомым параметрам. Причем делается это для единственного сечения, непосредственно примыкающего к тестируемому узлу. Есть, однако, более простой и более естественный способ определения параметров, входящих в выражение (1). Если координаты точек сечения заданы в системе главных осей сечения, то набор функций

,

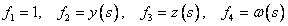стоящих в качестве множителей при искомых параметрах, обладает свойством “ортогональности”, т.е.

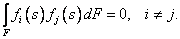
В частности из этого следует, что

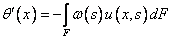.                                                                     (2)

На базе программного комплекса Selena [5] был разработан специальный режим, позволяющий в автоматическом режиме строить эпюры депланаций и бимоментов на конечноэлементных моделях стержней. Программа автоматически строит несколько сечений, перпендикулярных оси стержневого элемента и по формуле (2) вычисляет интегралы. Бимоменты вычисляются по формуле

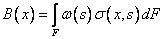
(здесь s(x,s) – нормальные напряжения в сечении). Такая автоматизация позволила проверить большое количество моделей узлов. В качестве примера приведем одну модель, представленную на рис.1. Толщины всех пластин, составляющих модель равны 1 см. Все три свободных конца стержневых элементов полностью защемлены.

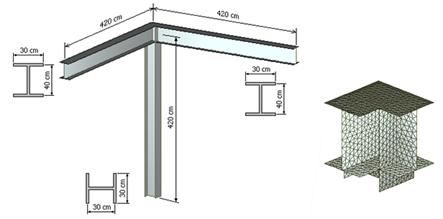
Рис. 1

На рис.2 показаны эпюры депланаций от единичных смещений конца одного из ригелей (размерность депланации - см^-1). Направления смещений и поворотов показаны на рисунках (рисунок 2d. соответствует единичной депланации).

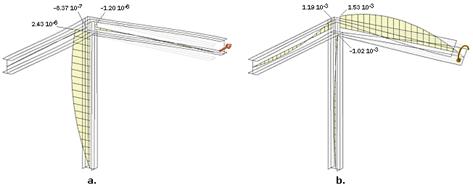
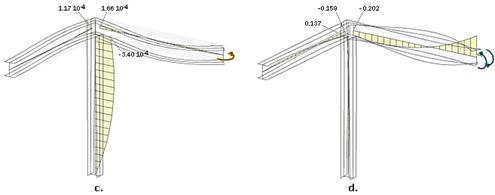
Рис. 2

Значения депланаций указаны в местах перехода регулярного сечения стержня в конструкцию узла. Как видно, ни о какой непрерывности депланации в узле говорить не приходится. То же самое подтверждают и множество других экспериментов. Лишь в частных случаях (неразрезных балок постоянного сечения и узлов простых Г-образных рам) наблюдается непрерывность депланации.

Перейдем к оценке влияния конструкции узла на перераспределение усилий в системе. Рассмотрим двутавровую балку с диафрагмой, делящей ее на две равные части (рис.3а).

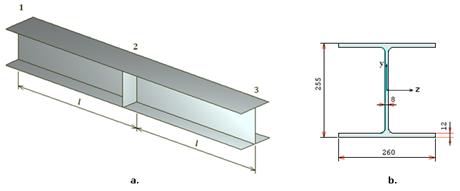
Рис. 3

Представим модель этой балки в виде соединенных между собой пары стержневых элементов с 7-ю степенями свободы в узле. Матрица жесткости каждого из этих стержней имеет вид

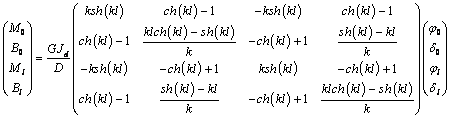                          (3)

(мы рассматриваем только те компоненты, которые ответственны за кручение и депланацию), где M₀,B₀,M₁,B₁ - крутящий момент и бимомент в начале и конце стержня, j₀,d₀,j₁,d₁ - угол поворота и депланация в начале и конце стержня (здесь и дальше депланацию будем обозначать буквой d), J_d,J_w - моменты инерции свободного кручения и секториальный момент инерции, D=kl∙sh(kl)-2[ch(kl)-1], 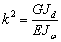. Сформируем матрицу жесткости системы, изображенной на рисунке 3а:

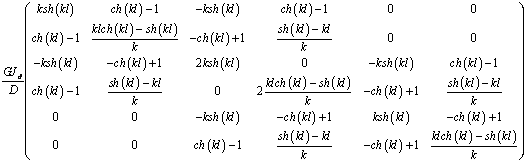                 (4)

(колонки матрицы жесткости соответствуют вектору переменных (j₁,d₁,j₂,d₂,j₃,d₃)). Очевидно, данная матрица абсолютно ни как не учитывает присутствие диафрагмы. Понятно, что в результате деформации, диафрагма будет “перетягивать”  на себя часть работы внешних сил. Причем, чем больше деформация, тем большая часть энергии будет запасаться в диафрагме. Учитывая характер общей деформации (перемещение концов стержня), энергия, запасенная в диафрагме, будет зависеть только от депланации узла №2. Т.е. диафрагма выполняет ту же роль по отношению к депланации, что и обычная упругая связь по отношению к перемещению или повороту. Иными словами, наша диафрагма – это упругая связь по отношению к депланации. Следовательно, часть бимомента, воспринимаемого диафрагмой, может быть представлена зависимостью

,

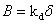где k_d - жесткость диафрагмы по отношению к депланации. Таким образом, вместо матрицы (4) мы должны записать

 (5)

Можно примерно оценить значение коэффициента k_d. Перемещение верхнего и нижнего контуров диафрагмы вдоль оси z (рис.4) можно описать выражением w=dw, 

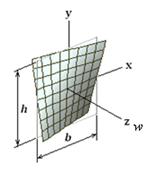
Рис. 4

где d – депланация сечения, а w – секториальная координата верхнего и нижнего обрезов сечения. Экстраполируя эту зависимость на поверхность всей диафрагмы в случае симметричного двутаврового сечения, для произвольной точки диафрагмы можно записать

.

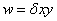Таким образом, диафрагма испытывает деформацию сдвига

,

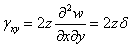где z – координата по толщине диафрагмы. Энергия деформации диафрагмы определяется выражением

,

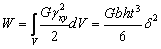где t – толщина диафрагмы (интегрирование выполняется по объему диафрагмы). В результате получаем

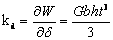.                                                                         (6)

Задавшись целью построить графики зависимости d=d(x) и B=B(x), найдем решение системы уравнений (5) для двух граничных задач:

1)       Единичный поворот правого конца: φ₁=0, d₁=0, φ₃=1, d₃=0. Выделяя из матрицы (5) третью и четвертую строки и решая соответствующую систему уравнений, получаем

2)        Единичная депланация правого конца: φ₁=0, d₁=0, φ₃=0, d₃=1. Аналогично имеем

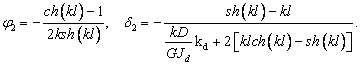
Рассмотрим эту задачу на конкретном примере. Возьмем двутавр ГОСТ 26029-83 26К1. Сечение имеет следующие характеристики: F=81.84 см², Jy=3515 см⁴, Jz=10170 см⁴, J_d=34.1 см⁴, J_=5.189∙10⁵см⁶, E=2.1∙10⁶кг/см², n=0.3. Ребру дадим толщину t=4 см. Вычисленная по формуле (6) жесткость ребра – k_d=1.0676∙10¹⁰кг∙см³. На рисунках 5а. и 5b. показаны расчетные кривые депланации и бимомента для задачи 1 (кривые помечены маркером “Теор.”). На рисунках 5с. и 5d. показаны аналогичные расчетные кривые для задачи 2.

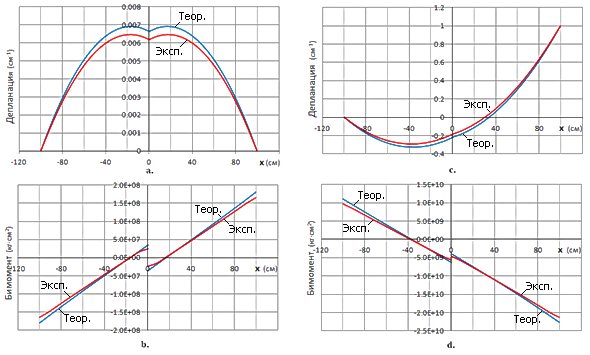
Рис. 5

Скачок бимомента связан с присутствием ребра жесткости в середине балки, а его значение точно соответствует формуле ∆B=k_dd. На тех же рисунках под маркером “Эксп.” показаны соответствующие графики, полученные в результате расчета конечноэлементной модели (рис.6а.).

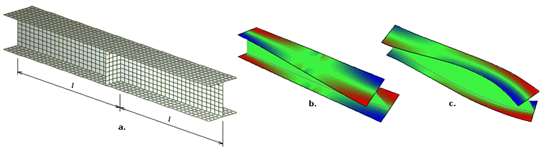
Рис. 6

На рисунках 6b. и 6c. показана картина деформации и продольные напряжения в нейтральном слое пластин, от единичного поворота (рис.6b.) и единичной депланации (рис.6c.) правого края балки. Как видно, теоретические и экспериментальные графики достаточно близки.

Понятно, что рассмотренный нами пример является вершиной упрощения поставленной задачи. На практике далеко не всегда удастся “вручную” оценить жесткость “депланационной пружины”, роль которой выполняют элементы конструкции узла. А также, если учесть, что депланация в общем случае терпит разрыв в узле, то понятно, что без исследования конечноэлементной модели узла эту проблему решить не удастся.

 Предположим мы построили такую конечноэлементную модель. Поставим обратную задачу – как на основе конечноэлементной модели определить жесткостные характеристики узла. Приведем наши рассуждения на примере все той же модели балки с диафрагмой (рис.6а.). Дадим концам нашей конечноэлементной модели балки единичные перемещения и построим матрицу единичных реакций – получим матрицу типа (3) размером 4х4. Исключим процедурой по Гауссу первые 3 переменные в этой матрице. В результате получим бимомент на правом конце свободно парящего в пространстве стержня от единичной депланации этого конца (нет ничего противоестественного, что стержень совершенно не закреплен – бимомент самоуравновешенная система сил). Понятно, что значение этой реакции является результатом сопротивления узла (диафрагмы) и реакцией напряженного состояния, возникающего в теле стержня. Естественно, чем короче будет наш стержень, тем меньше будет влияние его напряженного состояния на значение реакции и, в пределе, при длине стержня, стремящейся к нулю, реакция будет состоять только из сопротивления одной диафрагмы.

Продемонстрируем это на примере. Для чистоты эксперимента исследуем вначале эти утверждения на аналитической модели, представленной матрицей жесткости (5). Для определенности возьмем параметры все того же двутавра 26029-83 26К1 и той же диафрагмой толщиной 4 см. Задавшись определенной длиной стержней l, сформируем матрицу жесткости (5) и исключим из нее третью и четвертую строки. Это будет наша исходная матрица (матрица размером 4х4). Теперь исключим первые 3 строки из образовавшейся матрицы и, сделав несколько пересчетов при различных значениях параметра l, построим график зависимости реакции в последней связи от длины стержней l:

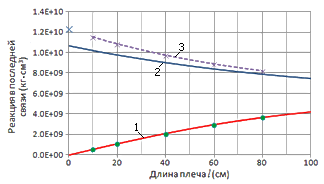
Рис. 7

Ккривая 1 на рис.7 соответствует стержню без диафрагмы и, естественно, при l→0 реакция от единичной депланации в центральном узле стремиться к нулю. Кривая 2 соответствует аналитическому решению для балки с диафрагмой, жесткость которой рассчитана по оценочной формуле (6). Нетрудно видеть, что реакция при l→0 стремиться точно к оценочному значению 1.0676∙10¹⁰ кг∙см³. Т.е. точно соответствует заданному k_d.

Вернемся теперь к конечноэлементной модели. Понятно, что ни о каком расчете узла со стержнями нулевой длины не может быть и речи. Разговор можно вести о нескольких пересчетах модели с разными длинами стержней с тем, чтобы построить предельный переход к нулевым длинам. Однако трудоемкость такой процедуры (многократное перестройка модели и ее пересчет), делает сомнительным ценность всего подхода. Однако, не стоит спешить.

Рассмотрим две модели одного узла, к которому подходят n стержней (рис.8).

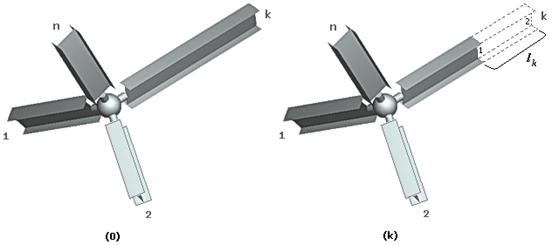
Рис. 8

Они отличаются тем, что k-й стержень модели (k) короче на величину, равную l_k. Рассмотрим две матицы единичных реакци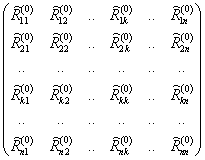й

     и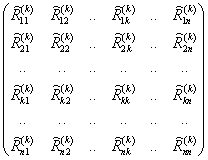   

(каждая из матриц 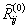и 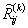 имеют размер 7х7 и представляет собой реакции в наложенных связях i-го узла от единичных смещений связей j-го узла). Первая матрица соответствует состоянию (0), вторая - состоянию (k) (см. рис.8). Попробуем получить из матрицы (k) матрицу (0). Для этого присоединим к k-ому элементу системы (k) стержень l_k. Обозначим собственную матрицу жесткости стержня l_k - :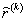

,

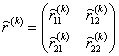а новому узлу дадим номер 0. Образованная новая матрица будет иметь вид (A). Поменяем местами нулевые и k-тые столбец и стоку – в результате матрица (A) преобразуется в матрицу (В):

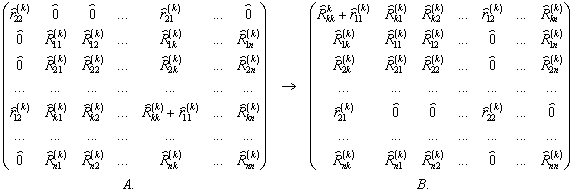
Если теперь исключить нулевую строку в матрице (В), то в результате, мы должны получить матрицу (0). А обращая эти равенства, выражаем компоненты матрицы (k) через компоненты матрицы (0):

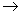
Если надо “укоротить” несколько элементов, то, не ограничивая общности, перенумеровав элементы в порядке их “укорочения”, получаем рекуррентную формулу (порядок “укорочения” не имеет значения)

                                     (7)

Таким образом, достаточно построить только одну конечноэлементную модель узла, а все остальные могут быть получены из исходной посредством рекуррентных формул (7). При этом, конечно, следует воспользоваться аналитическим представлением матрицы 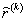, что представляется вполне естественным. На рис.7 кружками показаны несколько точек, соответствующих различным длинам плеч нашей неразрезной балки (рис.6a.) в случае отсутствия ребра жесткости (кривая 1), вычисленные на основе такой гибридной методики. Как видно, маркеры практически точно ложатся на кривую, полученную аналитически. Аналогичный расчет также был проделан и для балки с ребром (крестики, объединенные пунктирной линией – кривая 3). Как видно, результаты этих испытаний несколько отличаются от кривой, полученной аналитически (кривая 2). В этом нет ничего удивительного. Для аналитического построения изначально было задано значение жесткости диафрагмы k_d=1.0676∙10¹⁰ кг∙см³, полученное на основе эвристической оценки (6). В него же и “попала” аналитически построенная кривая при l→0. То, что экспериментальная кривая отличается от аналитической говорит только о том, что оценочное значение k_d не совсем верное, а истинную жесткость диафрагмы получаем экстраполяцией экспериментальной кривой до оси ординат, что дает k_d=1.2273∙10¹⁰ кг∙см³.

В рассмотренном выше примере конструкция узла обеспечивала равенство депланации подходящих к нему стержней. В общем же случае, как показывает опыт, депланации подходящих к узлу элементов могут быть различными. Обобщая все вышесказанное, мы можем предположить, что конструкция узла не только выполняет роль внешней деплационной связи, но и обеспечивает некоторое упругое взаимодействие между депланациями подходящих к нему стержней. Таким образом, узел можно рассматривать как некоторый одноточечный конечный элемент с n депланационными степенями свободы (по числу подходящих к узлу элементов). Т.е. собственную матрицу жесткости узла можно представить в виде

,   где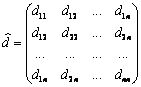        

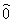( - нулевая матрица размером 6х6 и 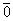 - нулевой вектор, состоящий из 6-и элементов). При этом процедура построения матрицы жесткости узла становится еще проще – достаточно исключить из матрицы жесткости конечноэлеметной модели только те строки, которые соответствуют перемещениям и вращениям и экстраполировать результат к отметке l=0.* Если узел обеспечивает равенство депланаций, то это значит, что связь между депланациями абсолютно жесткая. Это будет проявляться в том, что значения коэффициентов матрицы жесткости узла при l→0 будут стремиться к бесконечности. В этом случае процедуру исключения следует довести вплоть до последней депланационной переменной, а общее число депланационных переменных узла сократить (как было сделано в случае с нашей неразрезной балкой).

На рис.9b. показаны графики зависимости единичных реакций депланации (d₁₁, d₁₂, d₂₂) в зависимости от длины плеча Г-образной рамы, изображенной на рис.9а. Как видно, все 3 графика “дружно” устремляются к 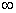 при l→0 (левая шкала).

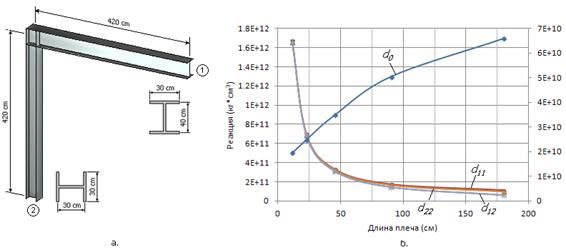
Рис. 9

Это типичное поведение реакций, если между депланациями сечений подходящих к узлу существует абсолютно жесткая связь. И, следовательно, для данного узла достаточно ввести только одну деплационную степень свободы. Жесткость узла по отношению к депланации определим, сделав последнее исключение

_______________________________________________________________________________________

*Если к узлу подходят n элементов, то достаточно исключить связи, наложенные на n-1 элемент – реакции, соответствующие перемещениям и вращениям n-го элемента окажутся нулевыми автоматически.

.

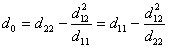Это и есть жесткость “внешней” депланационной связи, наложенной на узел. График зависимости жесткости d₀ от длины плеча показан на рис.9b. (правая шкала). Экстраполируя кривую к отметке l→0, получаем значение жесткости d₀=1.3911∙10¹⁰ кг∙см³.

Ниже на рис.10 показаны эпюры депланации  рамы от различных единичных смещений свободного конца стержня №1.

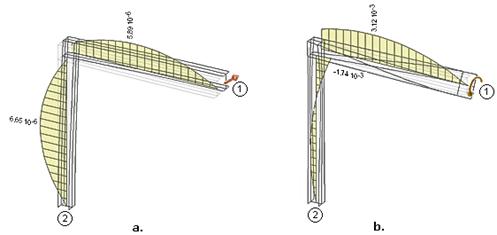
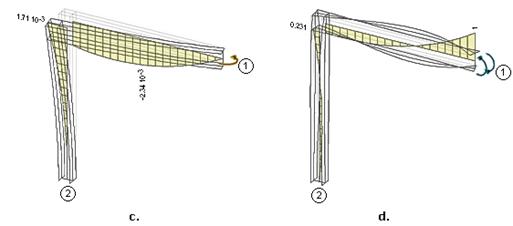
Рис. 10

В таблице 1 даны значения депланаций (в см^-1)стержней в точке соединения, "снятые" с экспериментальных эпюр (две колонки, объединенных заглавием “ Конечноэлементная ”). Эпюры депланации построены экспериментально на основе расчета конечноэлементной модели. График строится на участке от свободного конца стержня до места примыкания к конструкции узла, а значения депланаций в узле получены экстраполяцией графиков.

Таблица 1

В этой же таблице приведены значения депланаций в узле стержневой модели, полученные аналитическим путем. При формировании матрицы жесткости стержневой модели были использованы обычные формулы, а жесткость узла учтена добавлением к диагональной депланационной компоненте центрального узла значения d₀.

Приведем менее очевидный пример. Рассмотрим неразрезную балку, составленную из двух стержней одинакового сечения, но повернутых друг по отношению к другу на 90° (рис.11a.). Соединительная диафрагма имеет толщину 2 см.

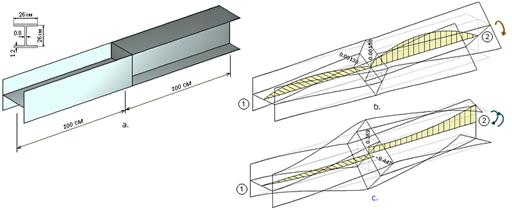
Рис. 11

Защемим оба конца балки и дадим единичный поворот правого конца балки (рис.11b.)  и единичную депланацию (рис.11c.). На рисунках 11b. и 11c. показаны эпюры депланации рассчитанные на основе конечноэлементной модели (эпюры строятся в плоскости наибольшего момента инерции сечения). Интересно отметить, что если в случае единичного поворота значения депланации обоих стержней в узле одинаковы, то в случае единичной депланации правого конца значения депланаций стержней в узле не только различны, но и имеют противоположные знаки.

На рис.12 показаны диаграммы изменения единичных реакций депланации (d₁₁, d₁₂, d₂₂) в зависимости от длины плеч неразрезной балки, полученные в результате процедуры, описанной выше.

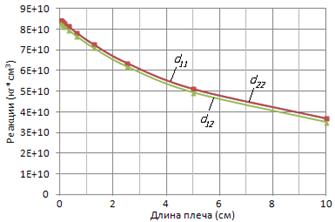
Рис.12

Как видно, при l→0 реакции стремятся к вполне конечным значениям: d₁₁= d₂₂=8.431∙10¹⁰ кг∙см³ и  d₁₂=8.289∙10¹⁰ кг∙см³. Т.е. в данном случае центральный узел должен рассматриваться как узел с двумя независимыми депланационными степенями свободы. В таблице 2 даны значения депланаций стержней в точке их соединения, рассчитанные на основе конечноэлементной и стержневой моделям. При этом центральный узел рассматривался как узел с 8-ю степенями свободы, а жесткость узла учтена добавлением вычисленных  выше коэффициентов d₁₁, d₂₂ и d₁₂.

Таблица 2

Приведем в заключение результаты по трехстержневому узлу, показанному на рис.1. На рис.13а. показаны диаграммы изменения депланационных компонент матрицы жесткости этой конструкции в зависимости от длины плеч (длины всех трех плеч менялись параллельно).

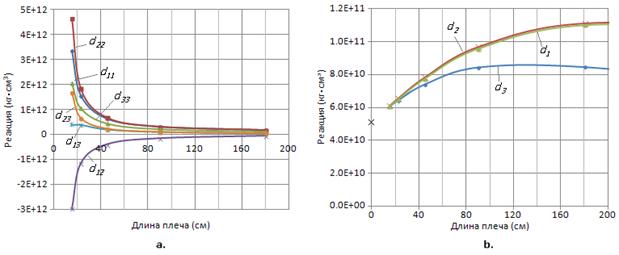
Рис. 13

Практически оказалось возможным “дотянуть” эти графики только до грани начала конструктивных элементов узла. Далее решение расходилось. Это, по-видимому, объясняется тем, что есть небольшое расхождение в значениях коэффициентов матрицы жесткости, полученных экспериментальным и теоретическим путем (напомним, что суть метода состоит в том, что экспериментально полученная матрица жесткости узла “укорачивается” при помощи аналитических формул). В то же время, если провести исключение вплоть до последнего элемента в матрице жесткости, то видно, что решение сходится к определенному пределу. На рис.13b. показаны три графика изменения последнего диагонального элемента матрицы, соответствующие трем вариантам выбора в качестве последнего одного из трех стержней. Все они, как видно, сходятся примерно к одному и тому же значению – около 5.1 10¹⁰ кг∙см³. Это значение и есть общая жесткость внешних деплационных упругих связей, наложенных на узел. Совпадение трех значений обусловлено тем, что жесткость депланационных связей внутри узла значительно больше, чем жесткость внешней связи.

В качестве первого приближения для коэффициентов матрицы жесткости узла можно выбрать значения реакций, полученных на последней успешной итерации. Как видно из рис.13а., последняя успешная итерация соответствует длине плеча 15 см. При этом будет происходить определенное искажение в значении коэффициента внешней упругой связи, которое мы знаем почти наверняка (в нашем случае, при таком выборе коэффициентов матрицы жесткости узла, значение внешней упругой связи окажется равным 6.05 10¹⁰ кг∙см³ – см. рис.13b.). Но скорее всего, учитывая общую приближенность всей нашей процедуры, такое искажение будет малосущественным.

В таблице 3 по каждому из трех стержней схемы, изображенной на рис.1, даны депланации в узле, полученные прямым расчетом конечноэлементной модели и методом, описанным выше.

Таблица 3

 В аналитической модели центральный узел рассматривался как объект с 9-ю степенями свободы, а собственная матрица жесткости узла была “снята” с графика на рис.13а. Как видно, обе группы значений достаточно близки. Можно предложить различные эвристические схемы улучшения решения. Но, как показывает наш опыт, благодаря тому, что жесткость депланационных связей внутри узла на два порядка выше, чем жесткость внешней депланационной связи, это уже мало что дает.

Таким образом, предложенная методика дает определенные основания на то, что проблема расчета конструкций, сформированных их тонкостенных стержневых элементов, может быть решена в рамках разумных приближений и без каких-либо надуманных ограничений. Платой за это является необходимость предварительного исследования конечноэлементной модели узла. Однако при современном уровне развития программного обеспечения это не является серьезной проблемой (тем более, что можно интегрировать в расчетные программные комплексы специализированные блоки для решения данной проблемы). Другим неприятным моментом является то, что в узле у нас появляется больше 7-и степеней свободы (в общем случае 6 плюс число подходящих к узлу стержней). Дополнительные сложности вызывает также и то, что даже связанные друг с другом узлы могут иметь различное число степеней свободы. Это усложняет и формирование, и обработку матрицы жесткости системы. Тем не менее, все эти трудности на сегодняшний день являются вполне преодолимыми.

Литература

1. Власов В.З., Тонкостенные упругие стержни / М.: Физматгиз, 1959, - 574 с.
2. Городецкий А.С., Здоренко В.С., Карпиловский В.С., Применение МКЭ к расчету тонкостенных стержневых систем // Сопротивление материалов и расчет сооружений. Вып. 28. – Издательство Будивэльнык, 1976. – С. 134-140.
3. Перельмутер А.В., Юрченко В.В., К вопросу расчета пространственных конструкций из тонкостенных стержней открытого профиля. – Сборник научных работ УкрНИИПСК. – Выпуск 13, 2014. – С.12-26.
4. Постнов В.А., Хархурим И.Я., Метод конечных элементов в расчетах судовых конструкций. М.: Судостроение, 1974. – 344 с.
5. Прочность, устойчивость, колебания. Универсальный программный комплекс для расчета конструкций на прочность. SELENA. 389 c.
6. Туснин А.Р., Численный расчет конструкций из тонкостенных стержней открытого профиля. – М.: Издательство АСВ, 2009. – 144 с.
7. Чернов С.А., К расчету пространственной тонкостенной стержневой системы / С.А.Чернов, И.Ф.Дьяков // Автоматизация и современные технологии. – 2008. - №2. – С.3-7.