Нормы расчета стержневых конструкций на устойчивость всегда базировалось на экспериментах, в которых, в подавляющем большинстве, испытанию подвергались стержни, закрепленные по шарнирной схеме опирания. Распространение теории на более сложные соединения стержней осуществлялось по теории так называемого “эквивалентного” стержня. То есть, каждому конкретному стержню ставился в соответствие шарнирно опертый стержень того же сечения, длина которого подбиралась таким образом, чтобы оба стержня теряли устойчивость при одном и том же значении сжимающей силы. К сожалению, несмотря на кажущуюся естественность такой аналогии, следует признать, что у данного подхода к решению проблемы устойчивости стержневых конструкций нет никакого ясного теоретического обоснования. Происхождение данного метода, скорее всего, связано с тем, что разработчики норм просто вынуждены были предложить хоть какую-то методику расчета стержневых конструкций. Учитывая уровень развития вычислительной техники, современный созданию норм, это, по-видимому, была единственная возможность подойти к решению данной проблемы. Однако при этом, одна трудно разрешимая проблема проверки устойчивости стержней, фактически подменялась другой не менее сложной – определением эквивалентных (расчетных) длин стержней. Все расчетчики знают, какие возникают трудности при определении расчетных длин элементов сложных стержневых конструкций. Применяемые в современных расчетных комплексах методы определения расчетных длин подчас дают столь фантастические результаты, что расчетчик всегда стоит перед делемой – верить или не верить результатам расчета. Таким образом, не вполне ясная научная теория подкреплялась еще менее ясным практическим методом.

В настоящей работе предлагается статистический подход к оценке устойчивости стержневых конструкций. Подход основан на ясных физических представлениях о природе данного явления и использует экспериментальную базу, заложенную в нормах проектирования стальных конструкций.

Согласно сложившемуся в настоящее время представлению о природе потери устойчивости стержневых конструкций, причиной того, что стержневые элементы теряют устойчивость при продольных усилиях меньших, чем это предсказывает теория Эйлера, является наличие малых начальных случайных искривлений и эксцентриситетов при прикреплении стержней. Поэтому, даже если стержень центрально сжат, в нем возникают изгибающие моменты и, если фибровые напряжения в какой-то момент превышают предел текучести материала, процесс потери устойчивости начинает развиваться с катастрофической скоростью. Если предположить, что начальное искривление меняется по синусоидальному закону, нетрудно получить формулу для предельного значения сжимающей силы, при которой в крайней фибре стержня появляется расчетное напряжение R_y

где A – площадь поперечного сечения стержня, а j – коэффициент, вычисляемый по формуле

где 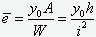- относительная начальная глубина неровности (здесь h – фибровое расстояние, i – радиус инерции сечения), а 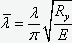- приведенная гибкость стержня.

Таким образом, если бы было известно предельное значение глубины начальной неровности стержня, по формуле (1) можно было бы вычислить предельное значение продольной силы, не превышение которой гарантировало бы отсутствие пластических деформаций. В европейских (Eurocode 3), американских, израильских, а также, с недавних пор, и в СП 16.13330.2011 и ДБН В.2.6-163:2010 для вычисления коэффициента j используется непосредственно формула (2). Разница состоит только в нормировании эксцентриситета 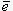. В российских нормах (СНиП II-23-81) нормируется непосредственно коэффициент j:

где .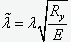

Обратим формулу (2), представив относительный эксцентриситет 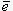как функцию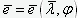

Воспользовавшись данными СНиП II-23-81, построим графики функции 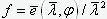для двух значений R_y=2050кг/см² и R_y=3250кг/см²:

Если учесть, что при одном и том же радиусе кривизны стержня стрела начальной неровности должна быть примерно пропорциональна квадрату его длины, такой характер изменения кривых 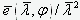кажется несколько странным. Очевидно, что результаты опытов заложенных в нормы одной начальной неровностью объяснить невозможно.

Введем в дополнение к начальной неровности эксцентриситет приложения силы (для упрощения будем считать, что эксцентриситеты с обеих сторон стержня имеют одну и ту же величину и направлены в одну сторону). Нетрудно показать, что максимальное плечо продольной силы в этом случае будет определено формулой

где y₀ – стрела начальной неровности, D – эксцентриситет, l – длина стержня, N – продольная сила, EI – жесткость стержня.

Составим выражение для максимального фибрового напряжения

где 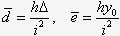. Пусть значение продольной силы таково, что фибровое напряжение достигает значения R_y. Введем обозначения

Тогда выражение (5) преобразуется к виду

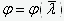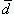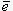Формула (6) позволяет построить зависимость при известных и . Как было подчеркнуто выше, стрела начальной неровности должна быть пропорциональна квадрату длины стержня. Поэтому представим выражение для 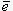в ви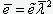де , где 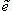- величина, зависящая только от R_y. Для относительного эксцентриситета нет такой ясности с выбором аналитической зависимости. Но, скорее всего, эксцентриситет установки стержня должен слабо зависеть от его длины и, при 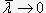, величина 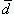также должна стремиться к нулю. Выберем простейшую зависимость для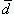

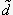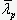где и - величины, зависящие только от R_y.

Подставляя введенные выражения для стрелы начальной неровности и эксцентриситета в уравнение (6), подберем коэффициенты 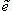, 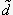и 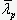так, чтобы решения уравнения (6) наилучшим образом приближались к значениям, вычисляемым по формуле (3). На рис.2 показаны графики зависимостей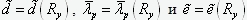

При R_y<3500кг/см² с достаточной точностью можно принять 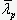=0.21, 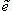=0.246, 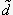=0.0223.

На рис.3 показаны графики зависимостей 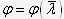, вычисленные в соответствии с формулой (3) (сплошная линия) и построенные на основе аппроксимации (пунктирная линия) при различных соответствующих значениях R_y

Как видно, предложенное разделение на начальную неровность и эксцентриситет дает хорошее совпадение с экспериментальными кривыми.

В актуализированной редакции СНиП II-23-81 СП 16.13330.2011, ДБН В.2.6-163:2010, а также нормах Eurocode 3 и нормах других стран нормируется непосредственно величина относительного эксцентриситета. В общем случае нормировка дается формулой

Аналогичный анализ позволяет вычислить коэффициенты 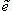, 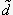и 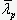для соответствующих значений факторов a и :

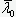Такой подход дает возможность проверить устойчивость стержневой конструкции следующим образом – введем в стержни начальные искривления и эксцентриситеты, амплитуды которых определены в соответствии с приведенной выше методикой, и рассчитаем конструкцию по деформированной схеме (расчет по деформированной схеме необходим, поскольку величина прогиба существенно зависит от продольной силы). Определим фибровые напряжения в стержнях. Если в каком-либо из сжатых стержней фибровые напряжения достигли или превысили R_y – это признак того, что данный стержень может потерять устойчивость.

Стержни можно включить в конструкцию двумя способами - сопрягая и не сопрягая углы поворота стержней в узлах. Включение стержней по схеме “с сопряжением углов поворота” можно представить следующим образом. На узлы конструкции накладываются связи, препятствующие поворотам. Перед присоединением каждый стержень выгибается так, чтобы его нейтральная ось представляла собой прямую линию – в таком виде стержень монтируется в систему. После того, как вся конструкция смонтирована, убираются связи, наложенные на узлы. При включении стержней по схеме “без сопряжения углов поворота”, стержни предварительно не выгибаются, а “привариваются” к узлам конструкции в естественном состоянии. Конструкции, собираемые на болтах, скорее следует рассчитывать по схеме “с сопряжением углов поворота”. Сварные конструкции – без сопряжения.

Основная проблема при формировании расчетной схемы состоит в задании величин и направлений начальных неровностей и эксцентриситетов для различных стержней. Поскольку эти величины по своей природе носят случайный характер, то естественный выход состоит в том, чтобы рассмотреть несколько выборок. Сделав несколько расчетов с различным распределением начальных несовершенств на одну и ту же нагрузку, путем статистической обработки результатов, можно сделать вывод о несущей способности конструкции.

Данный алгоритм был реализован на базе программного комплекса Selena*. Программа выполняет серию расчетов по деформированной схеме (число расчетов определяет пользователь), генерируя знаки и значения амплитуд неровностей и эксцентриситетов случайным образом. Предполагается, что глубины неровностей и эксцентриситетов распределены по нормальному закону в интервале [0,X], где X – предельное значение начальной неровности или эксцентриситета, определяемые в соответствии с изложенной выше методикой. Центр распределения находится в точке X/2. Стандарт распределения принимался равным X/5 (величина стандарта X/5 выбрана произвольно – исследования показали, что результат мало зависит от величины стандарта). В результате, по сформированным выборкам, для каждого стержня программа вычисляет математические ожидания и стандарты отклонения фибровых напряжений. На основе этих данных программа определяет для каждого стержня предельное фибровое напряжение сжатия, которое не будет превышено с заданной вероятностью. Сравнивая это напряжение с R_y, делается вывод о несущей способности стержня.

Чтобы оценить, насколько результаты статистического метода проверки устойчивости корреспондируются с принятой в настоящее время методикой расчета по эквивалентной гибкости, произведем расчет стержня двутаврового сечения длиной L=10 м и L=30 м, имеющего i=0.3274 м, h=0.8 м, E=2.1•10⁷ т/м², R_y=28500 т/м₂.

Ниже в таблице 1. напротив каждой расчетной схемы даны значения коэффициента свободной длины m, гибкости l=mL/i, коэффициента j, рассчитанного в соответствии со СНиП II-23-81, и значения критической силы N=jAR_y (значение критической силы вычислялось без учета коэффициента условий работы). Затем каждый из стержней был проверен на устойчивость по программе. При этом в качестве нагрузки прикладывалась сжимающая сила, рассчитанная по формуле N=jAR_y. Проверка состояла в следующем – если результаты расчета по обеим теориям совпадают, то расчет по программе для каждой из схем должен дать напряжение в крайней фибре равное или близкое к R_y.

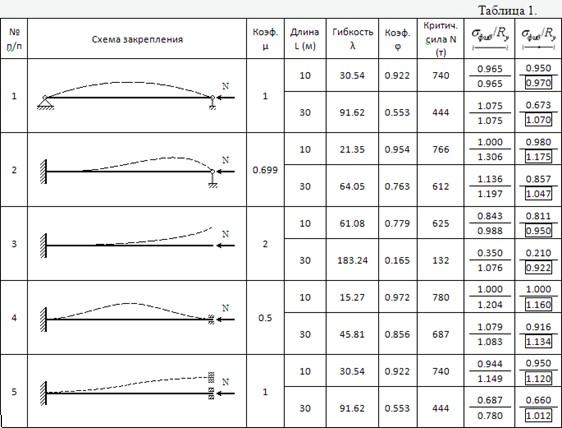
В предпоследней колонке таблицы приведены отношения N=s_фибр/R_y, посчитанные c вероятностью непревышения 99.9%. Значение в числителе соответствует креплению стержня по схеме “без сопряжения углов поворота”, в знаменателе – “с сопряжением”. Как видно, все схемы, за исключением консольного стержня (схема №3), присоединенного “без сопряжения углов”, а также схемы №5 для длинного стержня, дали неплохое совпадение с расчетом по СНиП. Причину отклонения 3-ей схемы нетрудно понять, если взглянуть на рис.4.

Очевидно, изгибающий момент от одной и той же силы по схеме а. будет приводить к меньшим фибровым напряжениям, чем по схеме b. Понятно, что схема b. куда лучше вписывается в теорию эквивалентного стержня (деформация консольного стержня при потере устойчивости описывается четвертью волны), поэтому и совпадение в этом случае лучше.

Причина заниженных фибровых напряжений по схеме №5 состоит в том, что неровность моделируется одной полуволной, что плохо вписывается в форму деформации стержня при потере устойчивости. Последняя колонка таблицы 1. содержит отношения s_фибр/R_y, посчитанные для тех же схем, с введенным промежуточным узлом. Благодаря тому, что на каждый из образовавшихся двух стержней программа накладывает неровности независимо друг от друга, возникают неровности соответствующие по форме двум полуволнам на всей длине стержня. Как видно, включение неровностей с двумя полуволнами дало очень хороший результат – все значения s_фибр/R_y для схемы “с сопряжением углов поворота” (в знаменателе обведено рамкой) очень близки к единице (среднее значение по всем схемам составляет 1.056, среднее квадратичное отклонение 0.086). Причем, одинаково хорошо описываются как короткие, так и длинные стержни.

Как и следовало ожидать, расчет по схеме “с сопряжением углов поворота” дает более высокий уровень напряжений. Это объясняется тем, что при сопряжении углов поворота в конструкции возникают дополнительные внутренние напряжения. Для коротких стержней (за исключением консольной схемы) расчеты по схеме “без сопряжения углов поворота” дает более близкий результат к расчету устойчивости по методике СНиП. Для длинных стержней результат существенно зависит от того, насколько хорошо одна полуволна неровности описывает реальную деформацию стержня. Включение неровностей, описываемых двумя полуволнами, дает хороший результат, как для коротких, так и для длинных стержней, включаемых по схеме “с сопряжением углов поворота”.

На рисунке 5. Показана расчетная схема 6-пролетной рамы. Ригели и стойки рамы сформированы из сечений D26020-83 16B2. Они имеют следующие характеристики: A=0.002009 м², I= 8.6929 106 м⁴, R_y= 28500 т/м², E= 2. 107 т/м². Высота рамы и шаг колонн - 4м. Расчет на общую устойчивость конструкции дал значение критического параметра – 2.71.

Рядом с каждой стойкой даны значения коэффициента свободной длины m (коэффициент дан из расчета полной высоты стойки), гибкости l и коэффициента j, вычисленному по нормам СНиП II-23-81. Ниже приведено значение критической силы, рассчитанной по формуле N_кр=j/RA.

На рис.6 показаны графики зависимости s_фибр/R_y по каждой из колонн в функции от значения критического параметра k.

В таблице 2 дано сравнение критических параметров по каждой из колонн, вычисленных на основании значений N_кр, рассчитанных в соответствием с нормами СНиП – k_СНиП (k_СНиП,i=N_кр,i/N_i) и значениями параметра k в момент прохождения соответствующего графика через значение s_фибр,i/R_y=1, вычисленными на основе изложенной выше теории (на рис.6 обведено кружками).

Как следует из таблицы, можно констатировать хорошее совпадение двух подходов. Причем, главные критические значения по статистической теории оказались ниже, чем предсказывает теория эквивалентного стержня.

На рис.7 показан результат проверки плоской рамной конструкции на устойчивость.

Все стержневые элементы, которые на схеме не подписаны, имеют сечение 2L75x6. Расчетное сопротивление стали R_y=2305 кг/см². Цветовая шкала справа показывает отношение R_y=2305 кг/см². Значения s_фибр/R_y вычислены из условия не превышения этих величин с вероятностью 99.9%. Те элементы, у которых s_фибр,i/R_y<-1, по устойчивости не проходят.

Заключение

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Е.И.Бритвин, А.А.Тарнопольский., К вопросу о проверке устойчивости стержневых конструкций. Науково-виробничий журнал "Будiвництво Украiни", №1, 2006 р., ст.22-27.
2. СП 16.13330.2011, Стальные конструкции, Актуализированная редакция СНиП II-23-81, Москва, 2011.