СТРОИТЕЛЬНАЯ МЕХАНИКА И РАСЧЕТ СООРУЖЕНИЙ ISSN 0039-2383 №2 2017, с.44-51
УДК 624.044
УРАВНЕНИЯ
ДЕФОРМАЦИИ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО
ПРОФИЛЯ
С УЧЕТОМ ДЕФОРМАЦИИ СДВИГА
Е.И.Бритвин, канд. физ.-мат. наук
|
Принято считать, что деформации сдвига мало влияет на напряженное состояние стержней. Заметным это влияние становится только у достаточно коротких стержней. В то же время, как было показано в ряде исследований, для тонкостенных стержней это влияние может быть весьма существенным уже для стержней средней длины. Особенно значимой проблема учета влияния деформации сдвига становится при попытке построить модель узла, образованного сочленением тонкостенных стержней [1], поскольку для адекватного описания модели требуется максимально точное соответствие аналитической и конечноэлементной моделей стержня. В настоящей работе получены уравнения деформации тонкостенных стержней открытого профиля с учетом деформации сдвига. Даны выражения для депланации и бимомента с учетом деформации сдвига. Приводятся формулы для вычисления коэффициентов сдвига различных сечений. Продемонстрирован эффект появления депланации в сечениях несимметричного тонкостенного стержня при смещении или повороте его концов без кручения. Аналитические решения проверены путем сравнения с результатами, полученными на конечноэлементных моделях.
|
В работе [1]
автором был предложен метод формирования матрицы жесткости узла сочленения
тонкостенных стержней. Узел рассматривается как одноточечный элемент с 6+n степенями
свободы (n - число
подходящих к узлу стержней). Реакции, соответствующие смещениям и поворотам
формируются обычным путем – накоплением реакций отдельных стержней,
рассчитанных аналитическим путем. Для вычисления компонент, соответствующих
депланационным степеням свободы, строится конечно-элементная модель узла. Формируются
компоненты матрицы жесткости, соответствующие единичным смещениям свободных концов
подходящих к узлу стержней. После чего, процедурой последовательного “укорочения”
стержней (процедура подробно описана в [1]), вычисляются все недостающие
реакции от единичных смещений n
депланационных степеней свободы. “Тонким местом” предложенной методики явилось
то, что окончательное решение получалось путем экстраполяции последовательности
таких “укорочений” к состоянию, соответствующему нулевой длине подходящих к
узлу стержней. При этом оказалось, что если конечно-элементная модель не вполне
адекватна аналитической (“укорочение” происходит путем аналитических
построений), то при приближении длин стержней к нулю, решение начинало
расходиться. С другой стороны, как показали исследования, если изначально сформировать
матрицу жесткости, соответствующую единичным смещениям свободных концов
стержней на основе аналитических решений, вводя в узел произвольные значения
депланационных компонент (матрица формируется путем исключения реакций
центрального узла), то процедура [1] возвращает точные значения заложенных
депланационных компонент. Несмотря на то, что во многих случаях достаточно было
взять решение вблизи “нуля”, актуальность проблемы соответствия аналитической и
экспериментальной моделей очевидна.
 Как
показал анализ [2], главным источником расхождения моделей является влияние
деформации сдвига. Так, например, для двутавра ГОСТ 26029-83 26К1 длиной 200
см расхождение в отдельных компонентах матрицы жесткости конечно-элементной и
аналитической модели без учета деформации сдвига от поперечных сил, достигала
43%. Учет деформации сдвига позволил снизить максимальную разницу между
компонентами матриц до 1.3%. В то же время максимальная разница между двумя
моделями в компонентах, соответствующих кручению и депланации оставалась
недопустимо высокой – более 7%. Таким образом, проблема влияния деформации
сдвига для данной задачи оказалась чрезвычайно актуальной. Можно указать целый
ряд работ, посвященных проблеме учета влияния деформации сдвига на работу
тонкостенных стержней. Сошлемся на работы [4]-[8]. Общим для всех
этих работ является то, что для построения разрешающих уравнений формируется
функционал энергии и затем, используя уравнения Лагранжа, формируется искомая
система уравнений. Следует отметить, что не всегда проведенный анализ оказывается
вполне корректным. Так, в работах [6], [8] уравнения состояния,
связывающие силовые факторы с деформациями, принимались на основе бессдвиговой
теории, что не вполне корректно. В других случаях уравнения получаются
столь сложными, что приходится ограничиваться частными решениями (Полусдвиговая
теория тонкостенных стержней [7]).
Как
показал анализ [2], главным источником расхождения моделей является влияние
деформации сдвига. Так, например, для двутавра ГОСТ 26029-83 26К1 длиной 200
см расхождение в отдельных компонентах матрицы жесткости конечно-элементной и
аналитической модели без учета деформации сдвига от поперечных сил, достигала
43%. Учет деформации сдвига позволил снизить максимальную разницу между
компонентами матриц до 1.3%. В то же время максимальная разница между двумя
моделями в компонентах, соответствующих кручению и депланации оставалась
недопустимо высокой – более 7%. Таким образом, проблема влияния деформации
сдвига для данной задачи оказалась чрезвычайно актуальной. Можно указать целый
ряд работ, посвященных проблеме учета влияния деформации сдвига на работу
тонкостенных стержней. Сошлемся на работы [4]-[8]. Общим для всех
этих работ является то, что для построения разрешающих уравнений формируется
функционал энергии и затем, используя уравнения Лагранжа, формируется искомая
система уравнений. Следует отметить, что не всегда проведенный анализ оказывается
вполне корректным. Так, в работах [6], [8] уравнения состояния,
связывающие силовые факторы с деформациями, принимались на основе бессдвиговой
теории, что не вполне корректно. В других случаях уравнения получаются
столь сложными, что приходится ограничиваться частными решениями (Полусдвиговая
теория тонкостенных стержней [7]).
В настоящей
работе, следуя алгоритму основателя теории тонкостенных стержней Власова В.З.,
будет получена система дифференциальных уравнения деформации
тонкостенных стержней открытого профиля с учетом деформации. На численных
примерах будет продемонстрировано хорошее совпадение получаемых решений с
экспериментом, а также будет показано, что полученные уравнения описывают
некоторые эффекты, невозможные с точки зрения стандартной теории. Вывод во
многом повторяет первоисточник [3]. Тем не менее, мы его проделаем целиком (в
сжатой форме), чтобы полученный результат не вызывал вопросов.
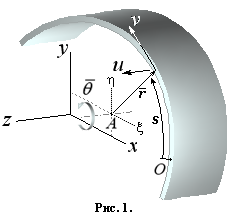
Представим
деформацию сечения в плоскости XY с продольной координатой z как сумму
поступательного перемещения 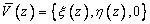 и
поворота сечения как твердого тела вокруг некоторого центра в точке A на угол
и
поворота сечения как твердого тела вокруг некоторого центра в точке A на угол 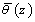 (Рис. 1). Тогда
перемещение точки, расположенной на срединной поверхности сечения с
координатами (x,y,z) можно
представить следующим образом
(Рис. 1). Тогда
перемещение точки, расположенной на срединной поверхности сечения с
координатами (x,y,z) можно
представить следующим образом
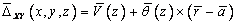 . (1)
. (1)
Выберем на
контуре сечения произвольную точку O и введем дуговую
координату точки (x,y,z), лежащей на
срединной поверхности сечения s –
расстояние до точки O вдоль дуги сечения. Перемещение
точки вдоль касательной к срединной поверхности равно
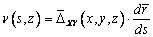 .
(2)
.
(2)
Деформация сдвига в плоскости оболочки связана с
равномерным по ее толщине касательным напряжением соотношением
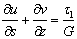 , (3)
, (3)
где t1 -
касательные напряжения в элементах сечения, образовавшиеся в результате действия
перерезывающих сил и стесненного кручения. Напряжение t1 складывается
из трех компонент:
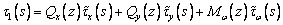 ,
(4)
,
(4)
где Qx, Qy и Mw - значения
перерезывающих сил и крутящий момент, ответственный за депланацию, а 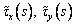 и
и 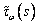 - эпюры
касательных напряжений от соответствующих единичных факторов. Учитывая,
что
- эпюры
касательных напряжений от соответствующих единичных факторов. Учитывая,
что 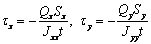 и
и 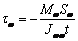 , где
, где 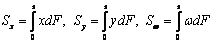 и t – толщина
оболочки,
имеем
и t – толщина
оболочки,
имеем
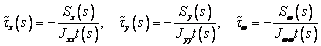 .
(5)
.
(5)
(во
избежание путаницы, мы снабдили моменты S.. и J..
индексами, соответствующими их подынтегральным выражениям). Подставляя (1) в
(2) и (2) в (3), после интегрирования по s, получаем
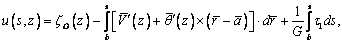
где b –
значение координаты s в некоторой
произвольной точке B, а штрихом
обозначено дифференцирование по переменной z. Очевидно, 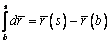 и
и 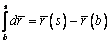 , где
, где 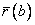 - радиус-вектор
точки B,
- радиус-вектор
точки B, 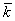 - единичный
вектор вдоль оси z и wa
–
секториальная координата точки контура сечения с началом отсчета в точке B,
вычисленная относительно центра, расположенного в точке A. Не
ограничивая общности, выберем точки A и B таким
образом, чтобы выполнялись условия
- единичный
вектор вдоль оси z и wa
–
секториальная координата точки контура сечения с началом отсчета в точке B,
вычисленная относительно центра, расположенного в точке A. Не
ограничивая общности, выберем точки A и B таким
образом, чтобы выполнялись условия 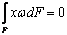 ,
, 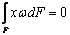 и
и 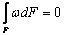 . В
результате выражение для продольных перемещений приобретает вид
. В
результате выражение для продольных перемещений приобретает вид
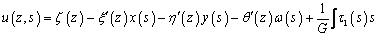 ,
,
где x(z), h(z) и z(z) – перемещения
точек, лежащих на оси, проходящей через точку А соответственно
вдоль осей x, y и
z. А x(s) и y(s) –
декартовы координаты точки сечения в главных осях. Последнее слагаемое в этой
сумме записано как неопределенный интеграл, поскольку перемещение u(z,s) определено с
точностью до аддитивной постоянной.
Поскольку
мы предполагаем, что напряжения вдоль образующей оболочки (в направлении
координаты s) и в
направлении, перпендикулярном поверхности оболочки равны нулю, нормальные
напряжения в сечении определяются выражением 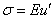 . Откуда
имеем
. Откуда
имеем
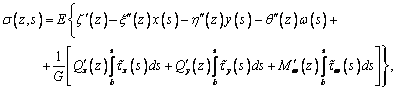 (6)
(6)
Подставляя
выражение (6) в уравнение равновесия 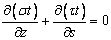 и
интегрируя по s,
получаем
и
интегрируя по s,
получаем
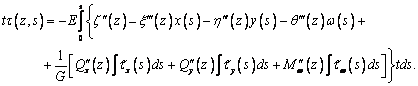 (7)
(7)
Запишем выражения для силовых факторов и депланации
(депланацию будем обозначать буквой d):
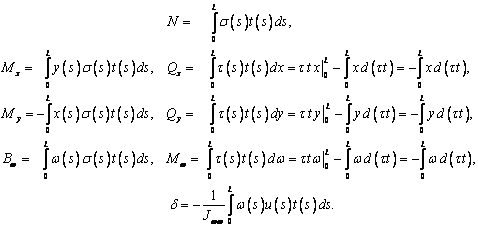
Здесь
в выражениях, содержащих произведение t(s)t(s) выполнено
интегрирование по частям и, поскольку мы предполагаем, что касательное
напряжение на торцах оболочки отсутствуют, первое слагаемое после
интегрирования по частям обращается в 0. Подставляя в эти выражения (6) и,
получаем
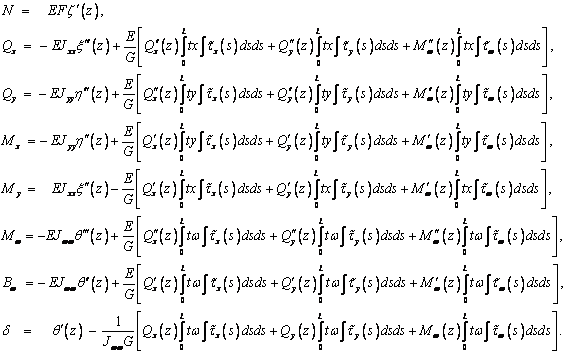
Двойные интегралы в этих выражениях преобразуем
интегрированием по частям и, учитывая выражения (5), имеем
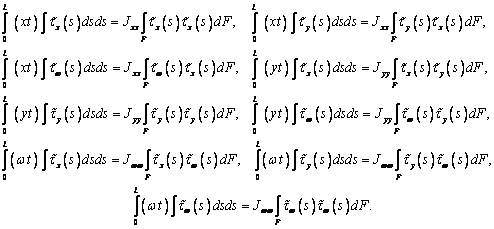 (8)
(8)
Введем обозначение 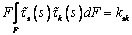 -
коэффициенты сдвига (F –
площадь
сечения, а индексы
s и k могут пробегать
значения x, y и w). Очевидно, ksk=kks. Если
сечение обладает симметрией относительно плоскости x=0, то
эпюры
-
коэффициенты сдвига (F –
площадь
сечения, а индексы
s и k могут пробегать
значения x, y и w). Очевидно, ksk=kks. Если
сечение обладает симметрией относительно плоскости x=0, то
эпюры 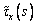 и
и 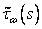 симметричны
относительно этой плоскости, а эпюра
симметричны
относительно этой плоскости, а эпюра 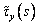 кососимметрична
и, следовательно, в этом случае kxy=kyx=0 и kyw=kwy=0. Аналогично, при симметрии
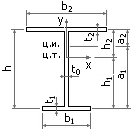
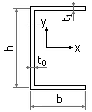
относительно плоскости y=0, имеем kxy=kyx=0 и kxw=kwx=0. В таблице 1 приведены формулы для
вычисления коэффициентов сдвига двутавра и швеллера.
кососимметрична
и, следовательно, в этом случае kxy=kyx=0 и kyw=kwy=0. Аналогично, при симметрии
относительно плоскости y=0, имеем kxy=kyx=0 и kxw=kwx=0. В таблице 1 приведены формулы для
вычисления коэффициентов сдвига двутавра и швеллера.
Таблица 1
|
Сечение
|
Коэффициенты сдвига
|
|
|
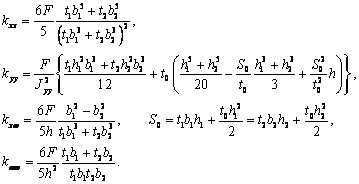
|
|
|
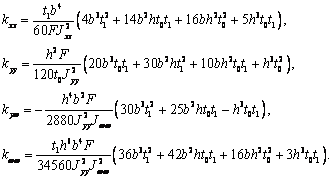
|
Теперь выражения
для силовых факторов и депланации можно переписать следующим образом
 (9)
(9)
Как видно, справедливы все
основные соотношения:
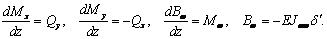 (10)
(10)
Учитывая,
что 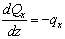 и
и 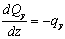 , из (9)
получаем
, из (9)
получаем
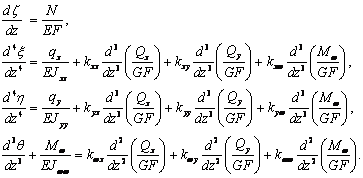 (11а)
(11а)
К этой системе уравнений надо добавить уравнение,
связывающее полный момент кручения Mz с моментами
свободного и стесненного кручения. Т.е.
 , (11b)
, (11b)
где
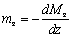 .
.
Рассмотрим один
частный, но важный случай - 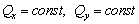 и
и 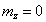 . Исключая
из четвертого уравнения (11а) и уравнения (11b) переменную θ,
получаем
. Исключая
из четвертого уравнения (11а) и уравнения (11b) переменную θ,
получаем
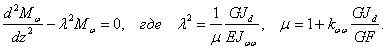
Его решение - 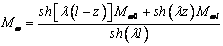 , где Mw0 и
Mwl – значения
момента Mw в начале и конце стержня. Подставив
это решение в (11b) и
интегрируя его, получаем
, где Mw0 и
Mwl – значения
момента Mw в начале и конце стержня. Подставив
это решение в (11b) и
интегрируя его, получаем
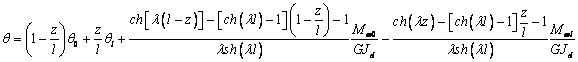 , (12)
, (12)
где q0 и ql
–
значения угла закручивания в начале и конце стержня.
Депланацию стержня вычислим по
последней формуле (9). Имеем
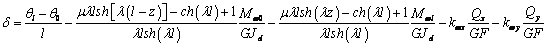 . (13)
. (13)
Из формул (11b) и (10)
находим выражения для момента кручения и бимомента:
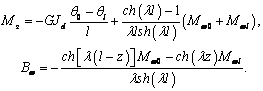 (14)
(14)
Формулы (12) и (13) дают возможность выразить
параметры Mw0 и Mwl
через
начальные и конечные значения переменных q и d - q0, d0, ql, dl:
 (15)
(15)
где 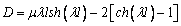 . Это позволяет
сделать функции q(z), d(z), Mz(z) и Bw(z) зависимыми
исключительно от этих четырех параметров.
. Это позволяет
сделать функции q(z), d(z), Mz(z) и Bw(z) зависимыми
исключительно от этих четырех параметров.
В работе [2] было
показано, что в тонкостенных стержнях несимметричного сечения при смещении или
повороте его концов (без кручения) возникает депланация. Изложенный выше
материал дает более строгое описание этого эффекта. Полагая в формулах (12), (13),
(14) q0=ql=0, d0=dl=0 и kwx≠0, kwy=0 (симметрия
относительно плоскости x=0), получаем
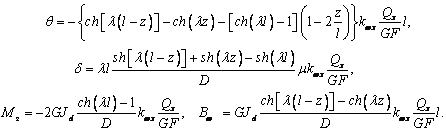 (16)
(16)
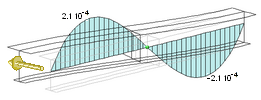
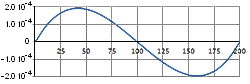
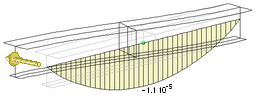
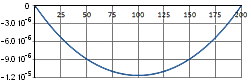
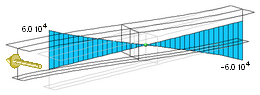
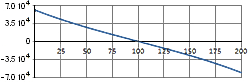
В таблице 2 приведены
кривые угла поворота, депланации и бимомента, возникающие в несимметричном
двутавре от единичного поперечного смещения левого конца (твутавр получен из
симметричного двутавра ГОСТ 26029-83 26К1 путем укорочения нижней полки в 2
раза; длина двутара – 200 см). Экспериментальные кривые получены на основе
расчета соответствующей конечно-элементной модели. Численные значения кривых
были рассчитаны путем проведения поперечных сечений и вычисления в их плоскости
соответствующих интегралов. Теоретические кривые были рассчитаны по формулам (16).
Таблицы 2
|
|
Экспериментальные кривые
|
Теоретические кривые
|
|
q
(рад)
|
|
|
|
d
(см-1)
|
|
|
|
Bw
(кг∙см2)
|
|
|
Решение (16) отличается от решения, полученного в
работе [2] тем, что оно учитывает деформацию сдвига от крутящего момента. Если
в формулах (16) положить m=1 и
l→0, то, как раз
придем к решению работы [2].
Задача
кручения тонкостенных стержней также претерпевает небольшие изменения. Ниже приводится
матрица жесткости задачи о кручении, рассчитанная на основе формул (14) и (15).
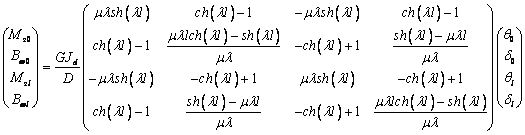 .
.
Отличие, как видно, состоит в присутствии множителя m (от которого также зависит детерминант D и сам
параметр l). Ниже
приводится сравнительная таблица 3 значений реакций все того же несимметричного
двутавра, приведенного в таблице 2 (длина двутавра – 200 см).
Таблица 3
|
Эксперимент
|
Теория без учета
деформации сдвига
|
Теория с учетом деформации
сдвига
|
|
q0
|
d0
|
ql
|
dl
|
q0
|
d0
|
ql
|
dl
|
q0
|
d0
|
ql
|
dl
|
|
Mx0
|
1.722
106
|
1.585
108
|
-1.722
106
|
1.585
108
|
1.799106
|
1.662
108
|
-1.800
106
|
1.662
108
|
1.715
106
|
1.577
108
|
-1.715
106
|
1.577
108
|
|
Bw0
|
1.585
108
|
2.172
1010
|
-1.585
108
|
9.978
109
|
1.662
108
|
2.252
1010
|
-1.662
108
|
1.072
1010
|
1.577108
|
2.167
1010
|
-1.577
108
|
9.874
109
|
|
Mxl
|
-1.722
106
|
-1.585
108
|
1.722
106
|
-1.585
108
|
-1.800
106
|
-1.662
108
|
1.800
106
|
-1.662
108
|
-1.715
106
|
-1.577
108
|
1.715
106
|
-1.577
108
|
|
Bwl
|
1.585
108
|
9.978
109
|
-1.585
108
|
2.172
1010
|
1.662
108
|
1.072
1010
|
-1.662 108
|
2.253 1010
|
1.577 108
|
9.874 109
|
-1.577108
|
2.167 1010
|
В
таблице 4 даны относительные погрешности значений реакций, рассчитанных без
учета и с учетом деформации сдвига относительно значений, полученных
экспериментальным путем.
Таблица 4
|
Теория без учета
деформации сдвига
|
Теория с учетом деформации
сдвига
|
|
q0
|
d0
|
ql
|
dl
|
q0
|
d0
|
ql
|
dl
|
|
Mx0
|
0.045
|
0.049
|
0.045
|
0.049
|
0.0041
|
0.0050
|
0.0041
|
0.0050
|
|
Bw0
|
0.049
|
0.037
|
0.049
|
0.074
|
0.0050
|
0.0023
|
0.0050
|
0.0104
|
|
Mxl
|
0.045
|
0.049
|
0.045
|
0.049
|
0.0041
|
0.0050
|
0.0041
|
0.0050
|
|
Bwl
|
0.049
|
0.074
|
0.049
|
0.037
|
0.0050
|
0.0104
|
0.0050
|
0.0023
|
Как
видно, максимальную относительную погрешность удалось понизить с 7% до 1%, что
может иметь решающее значение в плане соображений, приведенных в преамбуле
данной статьи.
Литература
- Бритвин Е.И., К расчету рамных конструкций, составленных из тонкостенных стержневых элементов / Строительная механика и расчет сооружений, 2016, № 4, С. 43-54.
- Бритвин Е.И., Формирование матрицы жесткости тонкостенных стержней с учетом влияния деформации сдвига / Строительная механика и расчет сооружений, 2016, № 5, С. 59-65.
- Власов В.З., Тонкостенные упругие стержни / М.: Физматгиз, 1959, - 574 с.
- Воробьев Л.Н., Влияние сдвига срединной поверхности на величину деформаций и напряжений в тонкостенных стержнях открытого профиля с недеформированным контуром [Текст] / Л.Н. Воробьев // Тр. Новочеркас. политехн. ин-та. — 1955. — Т. 26 (40).— С. 92–111.
- Мещеряков В.Б., Развитие теории тонкостенных стержней открытого профиля иее практические приложения [Текст] : дис. … д-ра техн. наук. — М. : МИИЖТ, 1974. — 317 с.
- Панасенко Н.Н., Юзиков В.П., Синельщиков А.В. Конечно-элементная модель пространственных конструкций из тонкостенных стержней открытого профиля в 2-х частях. Часть 1, Вестник АГТУ. Сер.: Морская техника и технология. 2015. №3, С. 89-100.
- Сливкер В.И., Строительная механика. Вариационные основы. – М.: Издательство ассоцоации строительных вузов, 2005. – 736 с.
- Юзиков В.П., Завьялова О.Б. Учет сдвига срединной поверхности при расчете тонкостенных стержней открытого профиля на статические и динамические воздействия. Научный потенциал регионов на службу модернизации. Астрахань: АИСИ, 2011. С. 69-75.