СТРОИТЕЛЬНАЯ МЕХАНИКА И РАСЧЕТ СООРУЖЕНИЙ ISSN 0039-2383 №1 2017, с.23-28
УДК 624.044
ФОРМИРОВАНИЕ МАТРИЦЫ
ЖЕСТКОСТИ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
С УЧЕТОМ ВЛИЯНИЯ
ДЕФОРМАЦИИ СДВИГА
Е.И.Бритвин, канд. физ.-мат. наук
|
На базе аналитического решения полной системы уравнений деформации тонкостенных стержней открытого профиля строится матрица жесткости элемента. Решение дается с учетом деформации сдвига как от поперечных сил, так и от крутящего момента, ответственного за стесненное кручение.
|
Принято считать, что деформация сдвига мало влияет
на напряженное состояние стержней. Заметным это влияние становится только у
достаточно коротких стержней. В то же время, как было показано в ряде
исследований, для тонкостенных стержней это влияние может быть весьма
существенным уже для стержней средней длины. Как было показано в работе [2], на
примере двутавра высотой 24 см и длиной 200 см, погрешность от игнорирования
деформаций сдвига в отдельных компонентах матрицы жесткости достигала 43%. В
той же работе был продемонстрирован еще более интересный эффект влияния
сдвиговых деформаций – появление депланации от поступательного смещения концов
стержня. Учитывая, что конечная цель всех этих построений – адаптировать теорию
тонкостенных стержней к реальному расчету конструкций, неизбежно возникает задача
построения как можно более точной матрицы жесткости тонкостенного стержневого
элемента. Проблема точности построения матрицы жесткости становится еще более
актуальна в рамках изысканий автора [1], где был предложен полуаналитический метод
формирования депланационных компонент реакций узла. Реализация метода,
оказалось, напрямую зависимой от точности построения матрицы жесткости
отдельного взятого тонкостенного стержня. В этой связи учет влияния деформации
сдвига стал для данной теории критически важным. В работах [4] и [5] приведен
алгоритм формирования матрицы жесткости тонкостенных стержней с учетом влияния
деформации сдвига. Алгоритм основан на формировании функционала энергии стержня
с подбором подходящих аппроксимаций функций деформации. Компоненты матрицы
жесткости находятся прямым дифференцированием функционала по концевым
перемещениям стержня. В настоящей работе строится матрица жесткости
произвольного (несимметричного) тонкостенного стержня на базе точного решения
уравнений деформации с учетом сдвигающих усилий, выраженного в квадратурах.
Как было
показано в работе [3], полная система уравнений деформации тонкостенного
стержня с учетом деформации сдвига, имеет вид
 (1)
(1)
Здесь z(z) -
продольные
перемещения центра тяжести сечения, x(z), h(z) -
поперечные перемещения точек, расположенных на оси, проходящей через центр
изгиба сечения соответственно, вдоль главных осей сечения x и y; θ(z) - угол
поворота сечения вокруг продольной оси; N, Qx и Qy –
продольная и поперечные силы в сечении; Mw – часть крутящего
момента, ответственная за стесненное кручение; F –
площадь поперечного сечения; Jxx и
Jyy - моменты
инерции, вычисленные относительно главных осей (индексы соответствуют
подынтегральным выражениям при вычислении моментов); Jd –момент
инерции свободного кручения; Jww - секториальный
момент
инерции, вычисленный относительно центра изгиба; коэффициенты ksr –
коэффициенты сдвига (см. [3]); qx, qy и mz –
распределенная нагрузка, приложенная вдоль оси, проходящей
через центр изгиба и распределенный крутящий момент.
Если положить 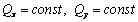 и
и
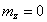 , то, решая совместно последние два уравнения
(1), имеем
, то, решая совместно последние два уравнения
(1), имеем
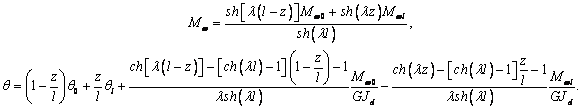 (2)
(2)
где, 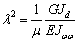 и
и 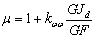 , а q0, Mw0 и ql, Mwl
–
значения
угла закручивания и крутящего момента Mw в начале и конце стержня.
Используя представление депланации
, а q0, Mw0 и ql, Mwl
–
значения
угла закручивания и крутящего момента Mw в начале и конце стержня.
Используя представление депланации 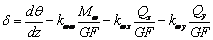 (см.[3]),
выразим моменты Mw0 и Mwl
через
значения депланации в начале и конце стержня d0 и dl:
(см.[3]),
выразим моменты Mw0 и Mwl
через
значения депланации в начале и конце стержня d0 и dl:
 (3)
(3)
(здесь 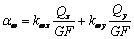 и
и 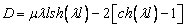 ). Вычислим полный момент
кручения Mz и
бимомент Bw по формулам Mz = GJdθ′+Mw
и Bw = -EJwwd′
). Вычислим полный момент
кручения Mz и
бимомент Bw по формулам Mz = GJdθ′+Mw
и Bw = -EJwwd′
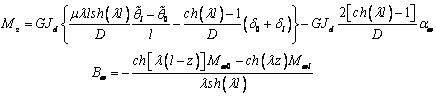
Откуда,
на концах стержня, получаем
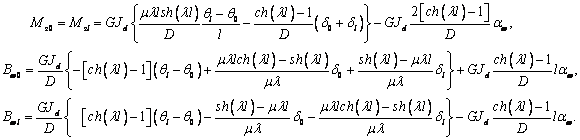 (4)
(4)
Перейдем к решению второго и третьего уравнений (1).
Поскольку в нашем случае также и 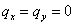 , второе
и третье уравнения (1) приобретают простой вид
, второе
и третье уравнения (1) приобретают простой вид
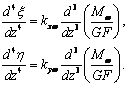 (5)
(5)
При этом надо
учесть, что наличие перерезывающих сил создает постоянный сдвиг по длине
стержня, выражающийся в дополнительном угле поворота сечений: для
переменной x - 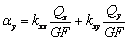 , для переменной
h -
, для переменной
h - 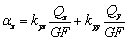 . Кроме того, дополнительный сдвиг
возникает и от действия крутящего момента Mw (это
видно из структуры уравнений (1)). Для переменной x он составляет: в начале стержня
. Кроме того, дополнительный сдвиг
возникает и от действия крутящего момента Mw (это
видно из структуры уравнений (1)). Для переменной x он составляет: в начале стержня 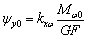 , в конце -
, в конце - 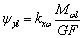 . И, соответственно,
для переменной h -
. И, соответственно,
для переменной h - 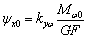 и
и 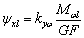 . Ситуация с углами ψ не
столь очевидна, как с углами ay и
ax, но анализ
показывает, что только при таком допущении можно получить симметричную по всем
компонентам матрицу жесткости стержня. Таким образом, уравнения (5) надо
решить при граничных условиях x(0)=x0, x(l)=xl, x’(0)=j0+ay+ψy0, x’(l)=j0+ay+ψyl и h(0)=h0, h(l)=hl, h’(0)=-f0+ax+ψx0, h’(l)=-f0+ax+ψxl.
. Ситуация с углами ψ не
столь очевидна, как с углами ay и
ax, но анализ
показывает, что только при таком допущении можно получить симметричную по всем
компонентам матрицу жесткости стержня. Таким образом, уравнения (5) надо
решить при граничных условиях x(0)=x0, x(l)=xl, x’(0)=j0+ay+ψy0, x’(l)=j0+ay+ψyl и h(0)=h0, h(l)=hl, h’(0)=-f0+ax+ψx0, h’(l)=-f0+ax+ψxl.
Проинтегрируем уравнения (5) при заданных граничных
условиях и вычислим значения перерезывающих сил по формулам (см. [3])
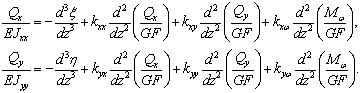
В результате имеем
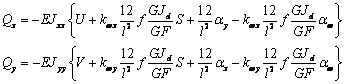 (6)
(6)
где
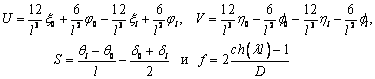 (7)
(7)
Подставляя в (6) выражения для ax, ay и
aω,
приходим к системе двух уравнений относительно Qx и
Qy. Решение
этой системы уравнений имеет вид:
 (8)
(8)
где
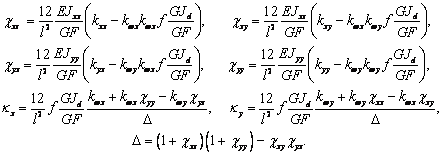 (9)
(9)
Изгибающие
моменты определим по формулам (см. [3])

И,
соответственно, в начале и конце стержня получаем:
 (10)
(10)
Выражения (4), (7), (8), (10) дают возможность
сформировать матрицу жесткости стержня. Процедура вычисления коэффициентов матрицы
достаточно громоздка. Мы приведем окончательный результат. Представим матрицу
жесткости в виде клеточной матрицы
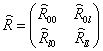
Матрица 
|
|
x0
|
h0
|
z0
|
f0
|
j0
|
q0
|
d0
|
|
Qx0
|
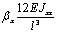
|
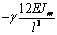
|
0
|
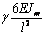
|
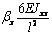
|
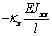
|

|
|
Qh0
|
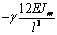
|
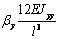
|
0
|
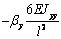
|
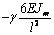
|
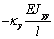
|
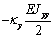
|
|
Nz0
|
0
|
0
|
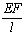
|
0
|
0
|
0
|
0
|
|
Mx0
|
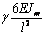
|
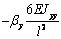
|
0
|
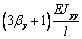
|
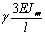
|
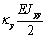
|
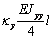
|
|
Mh0
|
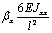
|
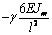
|
0
|
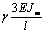
|
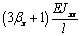
|

|
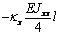
|
|
Mz0
|

|
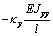
|
0
|
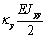
|

|
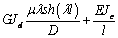
|
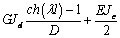
|
|
Bw0
|

|
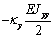
|
0
|
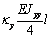
|
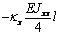
|
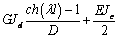
|
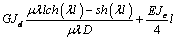
|
Матрица 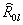
|
|
xl
|
h l
|
z l
|
fl
|
jl
|
ql
|
dl
|
|
Qx0
|

|
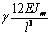
|
0
|
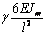
|
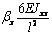
|
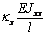
|

|
|
Qh0
|
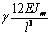
|
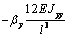
|
0
|
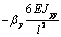
|
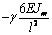
|
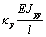
|
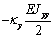
|
|
Nz0
|
0
|
0
|
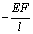
|
0
|
0
|
0
|
0
|
|
Mx0
|
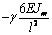
|
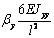
|
0
|
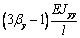
|
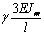
|
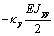
|
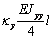
|
|
Mh0
|
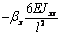
|
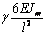
|
0
|
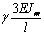
|
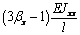
|
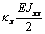
|
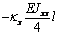
|
|
Mz0
|
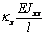
|
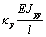
|
0
|
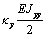
|

|
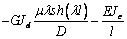
|
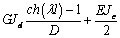
|
|
Bw0
|
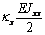
|
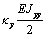
|
0
|
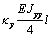
|
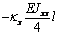
|
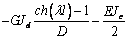
|
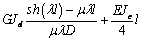
|
Матрица 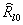
|
|
x0
|
h 0
|
z 0
|
f0
|
j0
|
q0
|
d0
|
|
Qxl
|
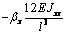
|
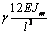
|
0
|
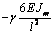
|
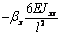
|
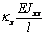
|
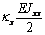
|
|
Qhl
|
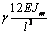
|
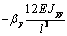
|
0
|
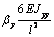
|
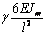
|
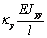
|
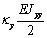
|
|
Nzl
|
0
|
0
|
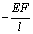
|
0
|
0
|
0
|
0
|
|
Mxl
|
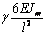
|
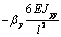
|
0
|
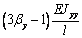
|
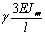
|
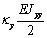
|
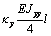
|
|
Mhl
|
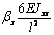
|
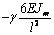
|
0
|
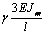
|
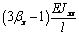
|

|
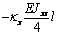
|
|
Mzl
|
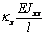
|
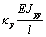
|
0
|
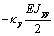
|
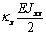
|
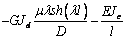
|
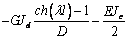
|
|
Bwl
|

|
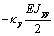
|
0
|
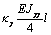
|
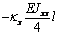
|
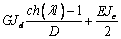
|
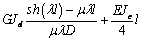
|
Матрица 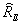
|
|
xl
|
h l
|
z l
|
fl
|
jl
|
ql
|
dl
|
|
Qxl
|
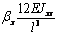
|
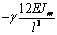
|
0
|
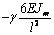
|
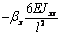
|

|
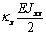
|
|
Qhl
|
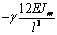
|
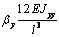
|
0
|
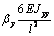
|
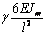
|
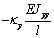
|
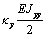
|
|
Nzl
|
0
|
0
|
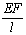
|
0
|
0
|
0
|
0
|
|
Mxl
|
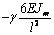
|
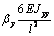
|
0
|
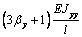
|
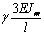
|
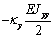
|
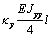
|
|
Mhl
|
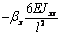
|
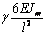
|
0
|
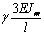
|
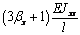
|
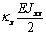
|
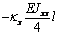
|
|
Mzl
|

|
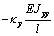
|
0
|
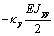
|
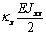
|
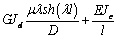
|
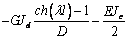
|
|
Bwl
|
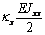
|
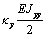
|
0
|
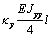
|
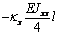
|
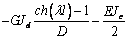
|
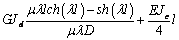
|
 Теперь
осталось сделать последний шаг – надо привести матрицу реакций к главным осям
сечения. Если центр изгиба совпадает с центом тяжести сечения, то построенная
выше матрица как раз и является решением проблемы. Если центр изгиба не
совпадает с центом тяжести, необходимо привести матрицу жесткости элемента к
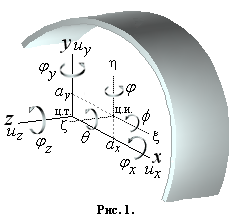
главным осям координат сечения. Пусть ux, uy, uz, jx, jy, jz –
перемещения точки, лежащей на оси, проходящей через центр тяжести сечения. Если
ax и ay – координаты
центра изгиба относительно главных осей, то справедливы следующие соотношения:
Теперь
осталось сделать последний шаг – надо привести матрицу реакций к главным осям
сечения. Если центр изгиба совпадает с центом тяжести сечения, то построенная
выше матрица как раз и является решением проблемы. Если центр изгиба не
совпадает с центом тяжести, необходимо привести матрицу жесткости элемента к
главным осям координат сечения. Пусть ux, uy, uz, jx, jy, jz –
перемещения точки, лежащей на оси, проходящей через центр тяжести сечения. Если
ax и ay – координаты
центра изгиба относительно главных осей, то справедливы следующие соотношения:
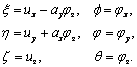
Таким образом,
матрица преобразования от переменных (ux, uy, uz, jx, jy, jz, d) к (x,
h, ζ, f, j, q, d) будет имеет
вид (d -
депланация сечения)
 .
.
Умножая
клетки матрицы жесткости стержня слева на транспонированную матрицу Â* и
справа на матрицу Â,
получаем искомую матрицу единичных реакций стержня в системе переменных (ux, uy, uz, jx, jy, jz, d)
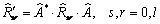 .
.
Литература:
- Бритвин Е.И., К расчету рамных конструкций, составленных из тонкостенных стержневых элементов / Строительная механика и расчет сооружений, 2016, № 4, С. 43-54.
- Бритвин Е.И., Влияние деформации сдвига на изгиб и кручение тонкостенных стержней. Строительная механика и расчет сооружений, 2016. №5. С. 59-65.
- Бритвин Е.И., Уравнения деформации тонкостенных стержней открытого профиля с учетом деформации сдвига, 2017. №2. С. 44-51
- Панасенко Н.Н., Юзиков В.П., Синельщиков А.В., Конечно-элементная модель пространственных конструкций из тонкостенных стержней открытого профиля в 2-х частях. Часть 1, Вестник АГТУ. Сер.: Морская техника и технология. 2015. №3, С. 89-100.
- Юзиков В.П., Завьялова О.Б., Учет сдвига срединной поверхности при расчете тонкостенных стержней открытого профиля на статические и динамические воздействия. Научный потенциал регионов на службу модернизации. Астрахань: АИСИ, 2011. С. 69-75.