СТРОИТЕЛЬНАЯ МЕХАНИКА И РАСЧЕТ СООРУЖЕНИЙ ISSN 0039-2383 №3 2017, с.36-45
УДК 624.044
О
КРУЧЕНИИ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ЗАМКНУТОГО ПРОФИЛЯ
Е.И.Бритвин,
канд. физ.-мат. наук
|
Работы по проблеме кручения тонкостенных стержней замкнутого профиля берут свое начало от 30-40-х годов прошлого века. Основоположными в этой области считаются работы А.А.Уманского. Математически теория А.А.Уманского очень близка к бессдвиговой теории тонкостенных стержней В.С.Власова, однако позволяет получить более или менее достоверный результат для тонкостенных стержней замкнутого профиля. Тем не менее, как показывают эксперименты, все же предсказания теории А.А.Уманского, подчас бывают очень далеки от действительности. В настоящей работе получены уравнения кручения тонкостенных стержней замкнутого профиля с учетом трех факторов: касательных напряжений свободного кручения, депланации и искажения формы сечения в своей плоскости. Дано аналитическое решение основных уравнений. Произведено сравнение предсказаний теории с теорией А.А.Уманского и с экспериментальными данными. Получено хорошее совпадение с экспериментом.
|
Проблема кручения тонкостенных стержней замкнутого
профиля постоянно привлекает к себе внимание исследователей. Наиболее фундаментальными
в этой области считаются работы А.А.Уманского [8], [9]. Также следует отметить
работы Ададурова Р.А., Джанелидзе Г.Ю., Пановко В.В. [4], [5], Бейлина Е.А. [1]
и других авторов. В последнее время, в связи с развитием вычислительной техники
и численных методов расчета, актуальность этой темы несколько снизилась. Тем не
менее, проблема остается остро востребованной, если речь идет о построении
модели стержневого элемента ([3], [7] и др.). К сожалению, как показывают
численные эксперименты, существующие модели кручения тонкостенных стержней
замкнутого профиля не всегда адекватно описывают реальный процесс деформации. В
настоящей работе предпринята попытка построить решение, более полно учитывающее
нюансы данной проблемы.
Будем считать, как принято в стандартной теории, что
при кручении сечения стержня не деформируются в своей плоскости. Тогда перемещение
произвольной точки сечения вдоль касательной к срединной поверхности сечения равно
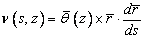 ,
(1)
,
(1)
где 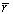 -
радиус-вектор, проведенный из центра изгиба, а q(z) –
угол
поворота сечения.
-
радиус-вектор, проведенный из центра изгиба, а q(z) –
угол
поворота сечения.
Нормальное к плоскости сечения перемещение u(s,z) и касательное
перемещение точки связаны соотношением
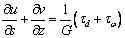 , (2)
, (2)
где td
– постоянное по толщине сечения касательное напряжение свободного кручения
(точнее, решение задачи о кручении при отсутствии нормальных напряжений), а tw
- касательные напряжения в элементах сечения,
вызванные действием стесненного кручения.
Пусть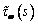 - эпюра касательных напряжений, от действия единичного момента стесненного кручения Mw(z), вызванного депланацией сечения, т.е.
- эпюра касательных напряжений, от действия единичного момента стесненного кручения Mw(z), вызванного депланацией сечения, т.е.
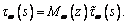 Для двухсвязного контура
Для двухсвязного контура 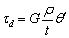 , где
, где
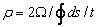 , а
W
- площадь контура. Подставляя (1) и выражения для
td
и
tw
в (2), после интегрирования, получаем
, а
W
- площадь контура. Подставляя (1) и выражения для
td
и
tw
в (2), после интегрирования, получаем
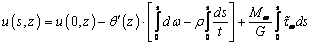 .
.
Введем обобщенную секториальную координату 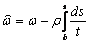 . Последнее выражение
приобретает вид
. Последнее выражение
приобретает вид
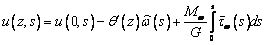 . (3)
. (3)
Поскольку u(z,s) и 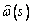 непрерывные по s функции,
то циркуляция напряжения
непрерывные по s функции,
то циркуляция напряжения 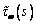 на замкнутом
контуре должна быть равна нулю. Т.е., должно выполняться условие
на замкнутом
контуре должна быть равна нулю. Т.е., должно выполняться условие
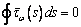 .
(4)
.
(4)
Если для сечений открытого профиля третье слагаемое
в выражении (3) рассматривается как приближение второго порядка (см. [2]), то
для сечений замкнутого профиля третье слагаемого нельзя рассматривать как
поправку к
базовому решению.
Ситуацию может облегчить то, что, как показывают численные эксперименты на
конечноэлементных моделях, продольные перемещения точек замкнутого контура с
большой степенью точности остаются пропорциональными эпюре 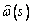 . Поэтому
заменим сумму первого и третьего слагаемых формулы (3) выражением
. Поэтому
заменим сумму первого и третьего слагаемых формулы (3) выражением
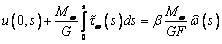 ,
(5)
,
(5)
где b - пока
неопределенный множитель, а F – площадь
сечения.
Таким образом, выражение (3) приобретает вид
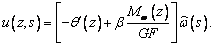 (6)
(6)
Поскольку
мы предполагаем, что напряжения вдоль образующей оболочки (в направлении координаты s) и в направлении, перпендикулярном поверхности
оболочки равны нулю, нормальные напряжения в сечении определяются выражением 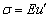 . Имеем
. Имеем
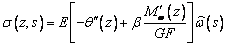 .
(7)
.
(7)
Подставляя это выражение в уравнение равновесия 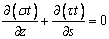 , и интегрируя
по s,
получаем
, и интегрируя
по s,
получаем
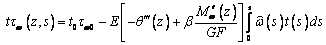 ,
(8)
,
(8)
где t0 и tw0 – толщина
стенки и касательное напряжение стесненного кручения в начальной точке дуги s. Выделяя в этом
выражении tw(z,s) и подставляя
его в (4), получаем
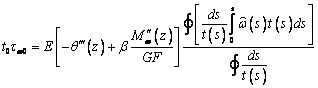 .
(9)
.
(9)
Крутящий момент
стесненного кручения определяется формулой
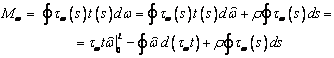
(здесь интервал [0,L] обозначают
начальную и конечную точки интегрирования на контуре). Первое слагаемое
в этой сумме обращается в 0, поскольку все три функции, образующие произведение
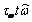 непрерывны на контуре. Последнее
слагаемое также обращается в 0 в силу соотношения (4). Таким образом,
окончательно получаем
непрерывны на контуре. Последнее
слагаемое также обращается в 0 в силу соотношения (4). Таким образом,
окончательно получаем
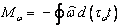 .
.
Подставляя в это выражение (8), получаем
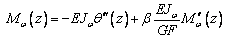 .
(10)
.
(10)
Учитывая
выражения (9) и (10), выражение для касательного напряжения (8) преобразуется к
виду
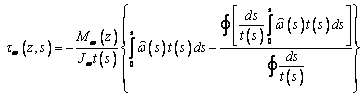 . (11)
. (11)
Не трудно убедиться, что это выражение не зависит от
выбора начальной точки интегрирования. Умножим равенство (5) на 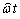 и проинтегрируем по контуру
сечения. Получим
и проинтегрируем по контуру
сечения. Получим
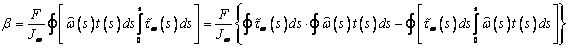 .
.
Очевидно, первое слагаемое в последней сумме
обращается в 0. Подставляя в это выражение (11), имеем
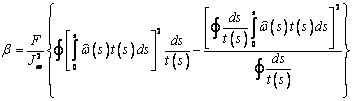 . (12)
. (12)
Для прямоугольного сечения (рис.1) в случае ta=tb=t

Рис.1
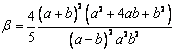 .
.
К уравнению (11) надо добавить условие постоянства
полного крутящего момента (предполагаем, что распределенный крутящий момент
отсутствует). В результате, после элементарных преобразований, получаем систему
уравнений
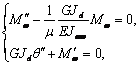 где
где 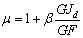 . (13)
. (13)
Это решение практически полностью совпадает с
решением А.А.Уманского [9], если вместо множителя 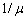 подставить
подставить 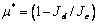 , где
, где 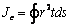 - направленный
полярный момент инерции (здесь r – плечо радиус-вектора,
перпендикулярного к ds и
проведенного из центра закручивания). Для прямоугольного сечения при ta=tb=t
- направленный
полярный момент инерции (здесь r – плечо радиус-вектора,
перпендикулярного к ds и
проведенного из центра закручивания). Для прямоугольного сечения при ta=tb=t 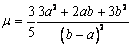 , а
, а 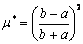 . На рис.2 показан
график зависимости
. На рис.2 показан
график зависимости 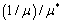 как функция
отношения сторон прямоугольника.
как функция
отношения сторон прямоугольника.

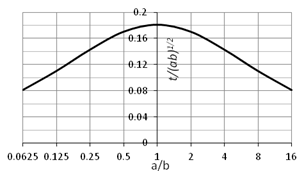
Рис.2 Рис.3
Как видно,
различие невелико. На рис.4 показаны решения уравнений (13) для прямоугольного
сечения с размерами: a=24см, b=48см, ta=tb=1см,
материал – сталь. Геометрические характеристики сечения: F=144см2, Jd=36864см4, Jw=442368см6. Параметры
депланации: b= 0.040625см-2,
m= 11.4
(параметр 1/m*=9 по теории А.А.Уманского). Расчеты были произведены для двух
длин стержня – L=200см и L=400см. Рассматривались две расчетные схемы: 1 – правый
конец стержня защемлен, левый конец поворачивается вокруг оси стержня на угол q=1,
депланация сечения отсутствует; 2 – правый конец стержня защемлен, на левый
конец накладывается деформация в продольном направлении по эпюре 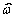 , поперечные
смещения отсутствуют. На рис.4 приведены графики депланации d и бимомента Bw (здесь и дальше под депланацией
мы будем понимать интеграл
, поперечные
смещения отсутствуют. На рис.4 приведены графики депланации d и бимомента Bw (здесь и дальше под депланацией
мы будем понимать интеграл 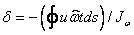 - именно
эта величина дуально сопряжена с бимоментом, вычисляемым по формуле
- именно
эта величина дуально сопряжена с бимоментом, вычисляемым по формуле 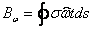 , а совпадает ли
она с первой производной угла закручивания – это уже второй вопрос.). Графики
рассчитанные в соответствии с изложенной выше теорией изображены тонкой
штриховой линией (
, а совпадает ли
она с первой производной угла закручивания – это уже второй вопрос.). Графики
рассчитанные в соответствии с изложенной выше теорией изображены тонкой
штриховой линией (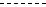 ).
Графики рассчитанные в соответствии с теорией А.А.Уманского – точечной (
).
Графики рассчитанные в соответствии с теорией А.А.Уманского – точечной (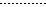 ). Там
же сплошной тонкой линией (
). Там
же сплошной тонкой линией ( ) показаны графики изменения тех же
величин, полученные на основе расчета конечноэлементных моделей. Расчет
производился по программе Selena [6]. Экспериментальные значения
депланаций и бимоментов вычислялись путем численного интегрирования по контурам
сечений, проведенных в тестируемых точках продольной оси стержня.
) показаны графики изменения тех же
величин, полученные на основе расчета конечноэлементных моделей. Расчет
производился по программе Selena [6]. Экспериментальные значения
депланаций и бимоментов вычислялись путем численного интегрирования по контурам
сечений, проведенных в тестируемых точках продольной оси стержня.
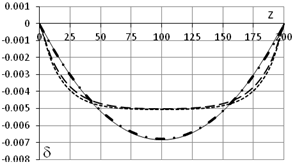
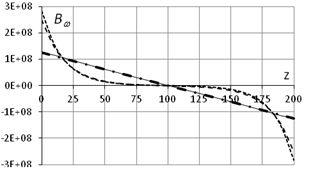
a. - d (L=200см, q0=1, d0=0) b. - Bw (L=200см, q0=1, d0=0)
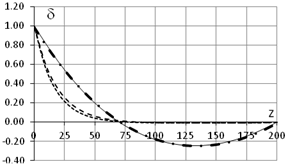
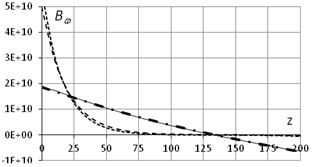
c. - d (L=200см, q0=0, d0=1) d. - Bw (L=200см, q0=0, d0=1)
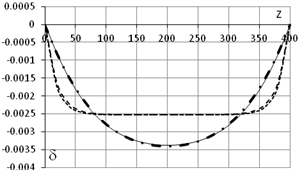
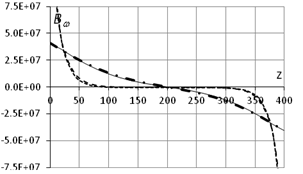
e. - d (L=400см, q0=1, d0=0) f.
- Bw (L=400см, q0=1, d0=0)
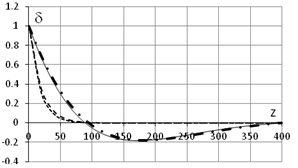
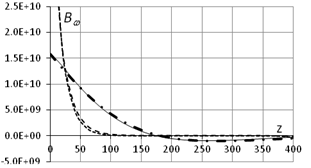
g. - d (L=400см, q0=0, d0=1) h.
- Bw (L=400см, q0=0, d0=1)
Рис.4
Ниже в
таблице .. приведены значения крутящих моментов, рассчитанные по обеим теориям.
Таблица 1
|
Длина стержня
|
Гран. усл.
|
А.А.Уманский
|
Теория
|
Эксперимент
|
|
L=200см
|
q0=1, d0=0
|
-1.517 108
|
-1.464 108
|
-1.510
108
|
|
q0=0, d0=1
|
-2.824
108
|
-2.504
108
|
-1.317
108
|
|
L=400см
|
q0=1, d0=0
|
-7.514 107
|
-7.381 107
|
-7.500
107
|
|
q0=0, d0=1
|
-1.399
108
|
-1.242
108
|
-4.317 107
|
Как
видно, обе теории очень близки друг к другу, но обе невероятно далеки от
реальности, причем и качественно и количественно. Слабым оправданием может
служить то, что все равно они намного лучше, чем, если “в тупую” применять
теорию тонкостенных стержней открытого профиля к стержням замкнутого профиля.
Причина
расхождения с экспериментом видна из рис.5. На рис.5a показана
деформация нескольких сечений стержня, один конец которого защемлен, а другой
повернут как твердое тело на заданный угол. На рис.5b показана
деформация того же стержня, на второй конец которого наложена деформация,
пропорциональная эпюре 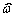 .
.
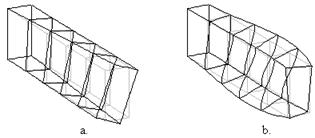
Рис.5
Бросается в
глаза существенная деформация искажения формы сечения в своей плоскости (особенно
это заметно на рис.5b),
которой, как известно, пренебрегает каноническая теория. Попытаемся учесть эту
деформацию. Вырежем мысленно фрагмент стержня, как показано на рис.6. Если бы
распределение
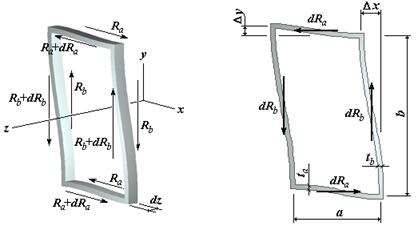
Рис.6
касательных
напряжений по контуру сечения не менялось вдоль оси стержня, то и не возникало
бы никаких сдвигающих усилий, стремящихся деформировать (исказить) контур в
своей плоскости. Но в нашем случае в сечении действуют две группы усилий –
касательные напряжения свободного кручения, распределенные по закону 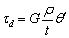 и касательные
напряжения стесненного кручения, распределенные по закону (11). Обе эти группы
напряжений меняются вдоль стержня, но таким образом, что суммарный момент
кручения от действия этих сил остается постоянным (мы рассматриваем случай
отсутствия распределенного момента вдоль оси стержня). В результате их
перераспределения в полоске сечения шириной dz возникает полностью
уравновешенная система сдвигающих усилий, приводящих к искажению сечения. В
случае прямоугольного сечения формула (11) дает следующее распределение
напряжений стесненного кручения в сегментах сечения от единичного момента Mw=1 (см. рис.1):
и касательные
напряжения стесненного кручения, распределенные по закону (11). Обе эти группы
напряжений меняются вдоль стержня, но таким образом, что суммарный момент
кручения от действия этих сил остается постоянным (мы рассматриваем случай
отсутствия распределенного момента вдоль оси стержня). В результате их
перераспределения в полоске сечения шириной dz возникает полностью
уравновешенная система сдвигающих усилий, приводящих к искажению сечения. В
случае прямоугольного сечения формула (11) дает следующее распределение
напряжений стесненного кручения в сегментах сечения от единичного момента Mw=1 (см. рис.1):
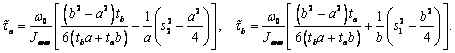
Интегрируя
эти напряжения по площади сегментов, получаем следующие значения
сдвигающих усилий:
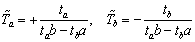
(для прямоугольного сечения  и
и 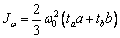 ).
).
Нетрудно также показать, что сдвигающие усилия от
единичного крутяoего
момента свободного кручения Md=1 составляют
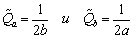
(они легко
находятся из условия tdt=const
вдоль контура сечения). Таким образом,
результирующие сдвигающие силы в элементах сечения составят
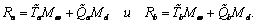
Учитывая, что Mw+Md=const,
на ширине dz
вырезанной полоски на каждый из сегментов действуют усилия

Пара сил dRa
создает
относительный сдвиг горизонтальных планок Dx,
который связан с dRa
соотношением 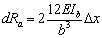 ,
где
,
где 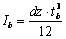 -
момент инерции изгиба вертикального звена (коэффициент 2 появился из-за того,
что сдвигу вдоль оси x сопротивляются
сразу 2 вертикальных звена). Аналогично, для
сдвига по вертикали получаем
-
момент инерции изгиба вертикального звена (коэффициент 2 появился из-за того,
что сдвигу вдоль оси x сопротивляются
сразу 2 вертикальных звена). Аналогично, для
сдвига по вертикали получаем 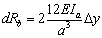 и
и
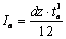 .
В результате получаем следующие выражения для относительных смещений
горизонтальных и вертикальных планок
.
В результате получаем следующие выражения для относительных смещений
горизонтальных и вертикальных планок
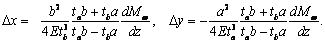 (14)
(14)
Таким образом, чтобы правильно учесть сдвиг, мы
должны в выражении (1) для касательных смещений точек сечения еще каким-то
образом добавить смещения (14). Введем в рассмотрение некоторую функцию 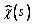 , такую, что на
горизонтальных полках величина
, такую, что на
горизонтальных полках величина 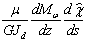 принимает
значение Dx, а на
вертикальных Dy. Эпюра функции
принимает
значение Dx, а на
вертикальных Dy. Эпюра функции 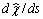 представлена на рис.7b.
представлена на рис.7b.
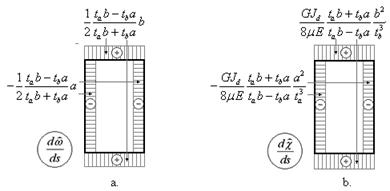
Рис.7
Теперь выражение
для перемещения
точки вдоль касательной к срединной поверхности приобретает вид
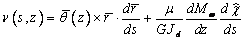 . (15)
. (15)
Воспользовавшись уравнением (2), приходим к
выражению для продольных перемещений (аналог уравнения (3))
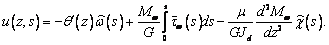 (16)
(16)
Проблематичность
данного уравнения состоит в том, что функция 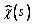 ,
вычисляемая как интеграл от
,
вычисляемая как интеграл от 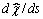 , совсем не
обязательно будет обладать такой же цикличностью, как и функция
, совсем не
обязательно будет обладать такой же цикличностью, как и функция 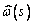 . Понятно, что
этот недостаток будет компенсирован вторым членом в правой части уравнения (16).
Но, чтобы добиться желаемого результата, мы пойдем на определенны подлог. На
рис.7 видно, насколько похожи друг на друга функции
. Понятно, что
этот недостаток будет компенсирован вторым членом в правой части уравнения (16).
Но, чтобы добиться желаемого результата, мы пойдем на определенны подлог. На
рис.7 видно, насколько похожи друг на друга функции 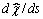 и
и 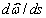 . Поэтому, как и
раньше, будем предполагать, что второй член в правой части уравнения (16)
пропорционален
. Поэтому, как и
раньше, будем предполагать, что второй член в правой части уравнения (16)
пропорционален 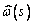 , а функцию
, а функцию 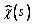 подменим
функцией
подменим
функцией 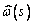 с некоторым
коэффициентом g,
который подберем таким образом, чтобы эти функции наименьшим образом отличались
друг от друга в смысле наименьших квадратов.. То есть, обеспечим
с некоторым
коэффициентом g,
который подберем таким образом, чтобы эти функции наименьшим образом отличались
друг от друга в смысле наименьших квадратов.. То есть, обеспечим
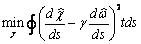 .
.
Прямое вычисление дает
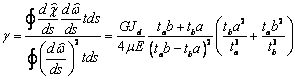 . (17)
. (17)
В результате, уравнение (16) приобретает вид
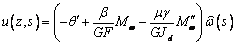 .
(18)
.
(18)
Далее, проходя по тем же пунктам, что и в первой
части работы, получаем следующие зависимости:
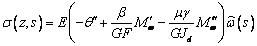 ,
(19)
,
(19)
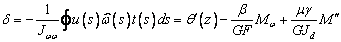 ,
(20)
,
(20)
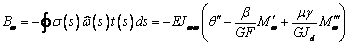 , (21)
, (21)
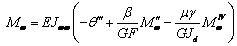 . (22)
. (22)
Выражения для касательных напряжений tw(s) (11) и для
коэффициента b (12) остаются в силе. К уравнению (22) надо добавить
условие постоянства полного крутящего момента
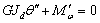 . (23)
. (23)
Исключая
при помощи (23) из уравнения (22) переменную q,
приходим к уравнению 4-го порядка относительно момента Mw
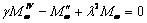 , (24)
, (24)
с характеристическим уравнением
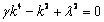 ,
(25)
,
(25)
где 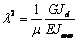 и
и 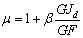 . Корни
уравнения (25) -
. Корни
уравнения (25) -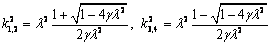 . Очевидно,
качество корней зависит от величины параметра
. Очевидно,
качество корней зависит от величины параметра 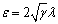 . Если
. Если 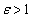 , то
, то 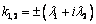 и
и 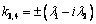 , где
, где 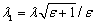 и
и 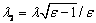 . Если
. Если
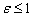 , то
, то 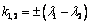 и
и 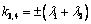 , где
, где 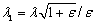 и
и 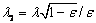 . Для
прямоугольного сечения в случае ta=tb=t параметр
. Для
прямоугольного сечения в случае ta=tb=t параметр 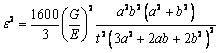 . На рис.3
показан график предельного значения
. На рис.3
показан график предельного значения 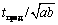 (соответствующего
значению e=1), как
функции отношения сторон прямоугольника a/b при G/E=1/2.6.
(соответствующего
значению e=1), как
функции отношения сторон прямоугольника a/b при G/E=1/2.6.
Как видно, случай e<1
достаточно маловероятен. Поэтому мы более детально рассмотрим случай
комплексных решений. Поскольку уравнение (24) имеет четвертый порядок, а
уравнение, составленное относительно переменной q - шестой, нам нужно еще два дополнительных условия
для решения этой задачи. Это является следствием того, что фактически к двум
стандартным переменным процесса закручиванию (twisting) и
депланации (warping)
добавилась еще одна переменная – искажение (distortion). Чтобы
остаться в рамках метода перемещений с моделью стержня с семью степенями
свободы в узле, будем искать только те решения, которые соответствуют смещениям
концов стержня без искажения. Очевидно, для этого нам следует положить M’w(0)=M’w(l)=0 (см. уравнение
(15)). Это требование, конечно, снижает вариабельность задачи, но, в конечном
счете, дает возможность получить некоторый практически значимый результат.
Опуская промежуточные выводы, приведем решения задачи, выраженные через
граничные значения момента Mw:
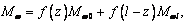 (26)
(26)
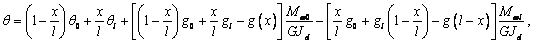 (27)
(27)
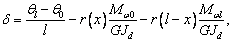 (28)
(28)
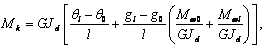 (29)
(29)
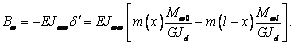 (30)
(30)
где функции f(z), h(z), d(z) и p(z) –
последовательные производные функции g(z), т.е. f(z)=gI(z), h(z) =gII(z), d(z)=gIII(z) и p(z)=gIV(z). Явный вид этих
функций представлен в таблице 2.
Таблица 2
|
|
Функция
|
|
g(z)
|
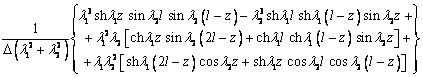
|
|
f(z)
|
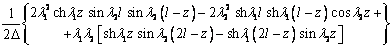
|
|
h(z)
|
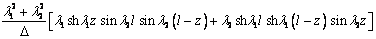
|
|
d(z)
|
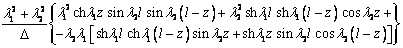
|
|
p(z)
|
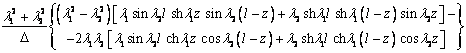
|
|
r(z)
|
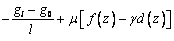
|
|
m(z)
|
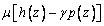
|
где 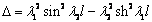 .
.
Используя уравнение (28), выразим моменты Mw0 и Mwl
через
значения угла поворота и депланации на концах стержня
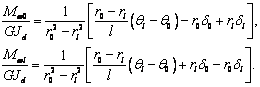 (31)
(31)
Эти соотношения
позволяют построить кривые изменения основных переменных задачи, параметрически
зависящих от смещений концов стержня q0, d0, ql,
dl,
а также построить матрицу единичных реакций стержня.
Для нашего прямоугольного сечения вычисления дают: g=1.119 105см2, l1=9.026 10-3cm-1, l2=8.775 10-3 cm-1. Рисунки 4
дополнены решениями, полученными по формулам (28), (30), (31) (жирная
штрихпунктирная линия 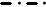 ). Как видно, расчетные кривые очень хорошо ложатся на кривые,
полученные экспериментальным путем.
). Как видно, расчетные кривые очень хорошо ложатся на кривые,
полученные экспериментальным путем.
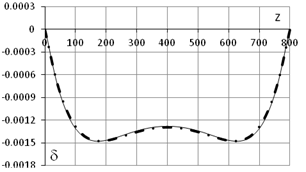
a. - d (L=800см, q0=1, d0=0) b. - Bw (L=800см, q0=1, d0=0)
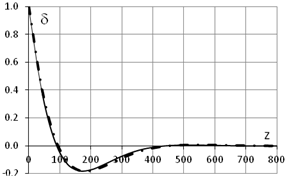
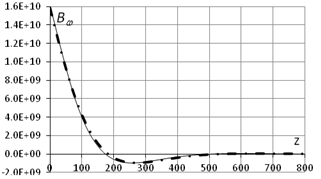
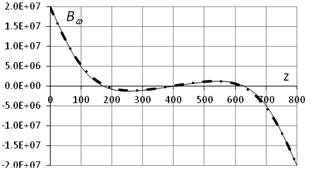
c. - d (L=800см, q0=0, d0=1) d. - Bw (L=800см, q0=0, d0=1)
Рис.8
Отметим еще один
интересный момент. Поскольку в решение задачи теперь входят тригонометрические
функции, то при значениях l2l>p можно ожидать, что
появятся волнообразные решения, что для задачи кручения стержней кажется
несколько неожиданным. Тем не менее, эксперимент, проделанный с тем же стержнем
коробчатого сечения, но длиной 800 см (l2l=7.020), подтвердил ожидания теоретических исследований. На рис.8
показаны кривые депланации и бимомента для коробчатого стержня сечением 24х48х1
см длиной 800 см. Здесь, как и раньше, сплошная тонкая линия – эксперимент,
жирная штрихпунктирная – теоретическая кривая. Ниже приводится сравнительная
таблица значений крутящего момента по всем шести экспериментам.
Таблица
3
|
Длина стержня
|
Гран. усл.
|
Теория
|
Эксперимент
|
|
L=200см
|
q0=1, d0=0
|
-1.501 108
|
-1.510
108
|
|
q0=0, d0=1
|
-1.266
108
|
-1.317
108
|
|
L=400см
|
q0=1, d0=0
|
-7.464
107
|
-7.500
107
|
|
q0=0, d0=1
|
-4.090 107
|
-4.317 107
|
|
L=800см
|
q0=1, d0=0
|
-3.727 107
|
-3.742 107
|
|
q0=0, d0=1
|
-1.981 108
|
-2.114 107
|
Как
видно, есть небольшое отклонение в экспериментах с наложением единичной
депланации. Тем не менее, этот результат неизмеримо лучше, чем результат,
приведенный в таблице 1.
Литература
- Бейлин Е.А., Вариант единой теории кручения тонкостенных стержней открытого, замкнутого и частично замкнутого профилей. Исследования по механике строительных конструкций и материалов. Киев: Будивельник, 1972. Вып.16, с.186-189.
- Бритвин Е.И., Уравнения деформации тонкостенных стержней открытого профиля с учетом деформации сдвига. Строительная механика и расчет сооружений. 2017, №2, с.44-51.
- Гуркова М.А., Кручение стержней открытого и замкнутого профиля и автоматизация процесса расчета. Дис. канд. техн. наук. М. 2000, 168с.
- Джанелидзе Г.Ю., Пановко Я.Г., Элементы строительной механики тонкостенных конструкций. М. Оборонгиз. 1952. 164с.
- Кан С.Н., Пановко Я.Г., Численный расчет конструкций из тонкостенных стержней открытого профиля. – М.: Издательство АСВ, 2009. – 144 с.
- Прочность, устойчивость, колебания. Универсальный программный комплекс для расчета конструкций на прочность SELENA. - 389с.
- Синельщиков А.В., Панасенко Н.Н., Математическая модель жесткостных характеристик тонкостенных стержней замкнутого профиля корабельных конструкций. Вес. АГТУ. Сер.: Морская техника. 2016. №2.
- Уманский А.А., Изгиб и кручение тонкостенных авиаконструкций. М. Оборонгиз. 1939.
- Уманский А.А., О нормальных напряжениях при кручении крыла самолета. ТВФ. 1940. №9.