СТРОИТЕЛЬНАЯ МЕХАНИКА И РАСЧЕТ СООРУЖЕНИЙ ISSN 0039-2383 №5 2016, с.59-65
УДК 624.044
ВЛИЯНИЕ ДЕФОРМАЦИИ
СДВИГА НА ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
Е.И.Бритвин, канд. физ.-мат. наук
|
На конкретном примере показано насколько важно при построении матрицы жесткости тонкостенных
стержней учитывать влияние деформации сдвига. Описан эффект появления депланации “без кручения”
для несимметричных сечений.
|
В работе [2] был предложен метод расчета рамных
конструкций составленных их тонкостенных стержневых элементов. Суть метода
состоит в том, что узел конструкции рассматривается как одноточечный конечный
элемент с n
дополнительными степенями свободы (по числу подходящих к узлу стержней). Центральным
моментом предложенного алгоритма является построение матрицы жесткости узла, в
основе которого лежит анализ конечноэлементной модели узла с последующим его
“обжатием” при помощи аналитических построений. Как было показано, метод
работает успешно, только в том случае, если аналитическая модель узла адекватна
конечноэлементной модели. Поэтому особую актуальность для предложенного метода
приобретает точность построения матрицы жесткости отдельно взятого стержня. В
настоящей работе на конкретном примере показано насколько важно при построении
матрицы жесткости для тонкостенных стержней учитывать влияние деформации
сдвига, а также описан эффект появления депланации “без кручения” для
несимметричных сечений.
Возьмем в
качестве примера двутавр ГОСТ 26029-83 26К1 длиной 200 см. Вычислим его
единичные реакции на основе конечноэлементной модели (рис.1) и параллельно
сделаем аналитический расчет.
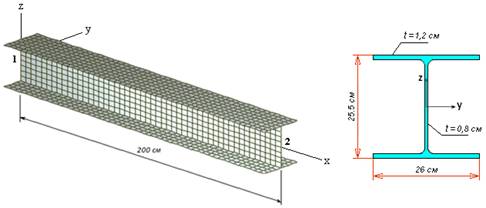
Рис.1
В
таблице 1 приведены значения реакций от единичных смещений концов стержня в
направлении оси z и
от поворота вокруг оси y,
полученные экспериментально и аналитическим путем.
Таблица 1
|
Эксперимент
|
Аналитический расчет
|
Относительная погрешность
|
|
uz1
|
jy1
|
uz2
|
jy2
|
uz1
|
jy1
|
uz2
|
jy2
|
uz1
|
jy1
|
uz2
|
jy2
|
|
Qz1
|
2.24 104
|
-2.24 106
|
-2.24 104
|
-2.24 106
|
3.20 104
|
-3.20 106
|
-3.20 104
|
-3.20 106
|
0.428
|
0.428
|
0.428
|
0.428
|
|
My1
|
|
3.31 108
|
2.24 106
|
1.17 108
|
|
4.27 108
|
3.20 106
|
2.14 108
|
|
0.290
|
0.428
|
0.829
|
|
Qz2
|
|
|
2.24 104
|
2.24 106
|
|
|
3.20 104
|
3.20 106
|
|
|
0.428
|
0.428
|
|
My2
|
|
|
|
3.31 108
|
|
|
|
4.27 108
|
|
|
|
0.290
|
Обращает
на себя внимание огромная разница между этими двумя примерами (последняя графа
таблицы). Причина этого расхождения состоит в том, что данный аналитический
расчет был произведен без учета влияния деформаций сдвига. Воспроизведем вывод
уравнения изгиба стержня с учетом деформаций сдвига. Нам этот результат
потребуется для дальнейшего изложения.
Уравнение
деформации стержня с учетом деформации сдвига имеет следующий вид
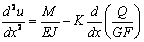 .
.
где K – коэффициент
сдвига, зависящий от форы сечения. При отсутствии распределенной нагрузки
решение этого уравнения сводится к решению однородного дифференциального
уравнения
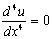 (1)
(1)
при граничных условиях u(0)=u0, u(l)=ul, u’(0)=j0-a, u’(l)=jk-a, где α – дополнительный
угол поворота концевых сечений, вызванный деформацией сдвига
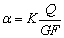 . (2)
. (2)
Очевидно, при
отсутствии распределенной нагрузки, угол a
будет
одинаковым с обоих концов стержня. Решая уравнение изгиба стержня (1) при
заданных граничных условиях, находим
 (3)
(3)
Из
соотношений Q=EJu’” и M=-EJu” , имеем
 (4)
(4)
Подставляя выражение для a (2) в первое из
этих выражений и, вводя обозначение
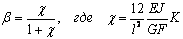 ,
(5)
,
(5)
после
несложных преобразований, получаем
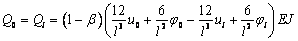 .
(6)
.
(6)
Подставляя
(2) и (6) во второе и третье выражения (4), получаем

Определение коэффициент сдвига K рассмотрим
на примере равнополочный двутавра (рис.2). Построим эпюры касательных
напряжений от сил Qy и Qz – ty(s) и tz(s) (нижний
индекс говорит о направлении действия перерезывающей силы).
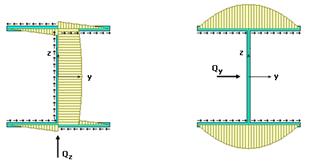
Рис.2
При чистом
сдвиге справедливы равенства
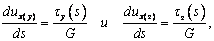
где ux(y) и ux(z) –
нормальные перемещения точек сечения от сил,
действующих в направлении осей y и z
соответственно. Из этих выражений находим
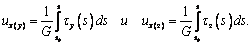 (7)
(7)
В качестве начальной точки s0 можно
выбрать любую точку сечения. Проведем наклонные плоскости 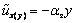 и
и 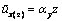 ,
подобрав коэффициенты αy и αz так,
чтобы эти плоскости наименее отклонялись от функций ux(y) и ux(z) в
смысле наименьших квадратов. Т.е.
,
подобрав коэффициенты αy и αz так,
чтобы эти плоскости наименее отклонялись от функций ux(y) и ux(z) в
смысле наименьших квадратов. Т.е.
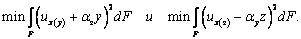
Минимизируя эти выражения по αy
и αz, получаем
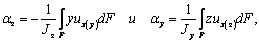 (8)
(8)
где 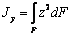 и
и 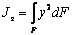 - моменты
инерции сечения.
Удобно
ввести новые характеристики
- моменты
инерции сечения.
Удобно
ввести новые характеристики
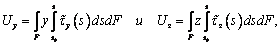 (9)
(9)
где 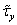 и
и 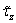 - касательные
напряжения в сечении от действия единичных перерезывающих сил в направлении
соответствующих осей.
Физический смысл этих характеристик – статический момент нормальных перемещений
от касательных усилий в элементах сечения. Тогда, учитывая (7), выражения (8)
можно переписать в виде
- касательные
напряжения в сечении от действия единичных перерезывающих сил в направлении
соответствующих осей.
Физический смысл этих характеристик – статический момент нормальных перемещений
от касательных усилий в элементах сечения. Тогда, учитывая (7), выражения (8)
можно переписать в виде
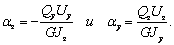 (10)
(10)
С другой стороны 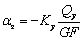 и
и 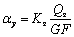 (см. выражение (2)).
Откуда имеем
(см. выражение (2)).
Откуда имеем
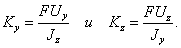 (11)
(11)
Заметим,
значения коэффициента сдвига K, вычисленные
по формуле (11) для сечений, заданных своим контуром, в точности совпадает со
значением, вычисленным по формуле 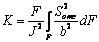 [1]. Для
нашего двутавра были получены следующие значения коэффициентов сдвига: Ky=1.574, Kz=4.628. В
результате пересчета с учетом влияния деформации сдвига, получаем
откорректированную матрицу реакций
[1]. Для
нашего двутавра были получены следующие значения коэффициентов сдвига: Ky=1.574, Kz=4.628. В
результате пересчета с учетом влияния деформации сдвига, получаем
откорректированную матрицу реакций
Таблица 2
|
Эксперимент
|
Аналитический расчет
|
Относительная погрешность
|
|
uz1
|
jy1
|
uz2
|
jy2
|
uz1
|
jy1
|
uz2
|
jy2
|
uz1
|
jy1
|
uz2
|
jy2
|
|
Qz1
|
2.24 104
|
-2.24 106
|
-2.24 104
|
-2.24 106
|
2.21 104
|
-2.21 106
|
-2.21 104
|
-2.21 106
|
0.013
|
0.013
|
0.013
|
0.013
|
|
My1
|
|
3.31 108
|
2.24 106
|
1.17 108
|
|
3.28 108
|
2.21 106
|
1.14 108
|
|
0.009
|
0.013
|
0.026
|
|
Qz2
|
|
|
2.24 104
|
2.24 106
|
|
|
2.21 104
|
2.21 106
|
|
|
0.013
|
0.013
|
|
My2
|
|
|
|
3.31 108
|
|
|
|
3.28 108
|
|
|
|
0.009
|
Таким образом, учет деформации сдвига позволил
практически сблизить результаты численного и аналитического эксперимента. Выполним
еще один расчет. Возьмем тот же двутавр, но нижнюю полку сделаем в 2 раза уже
(рис.3).
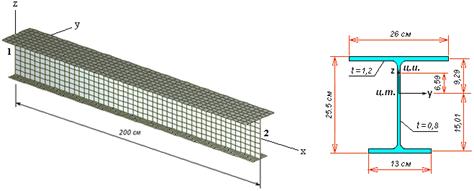
Рис.3
Расчет конечноэлементной модели дает неожиданный
результат
Таблица 3
|
uz1
|
uz1
|
uz1
|
jy1
|
jy1
|
jy1
|
d1
|
|
uz2
|
uz2
|
uz2
|
jy2
|
jy2
|
jy2
|
d2
|
|
N1
|
6.98 105
|
|
|
|
3.44 103
|
|
|
|
-6.9 105
|
|
|
|
-3.4 103
|
|
|
|
Qz1
|
|
5.99 103
|
|
-3. 9 104
|
|
5.99 105
|
6.15 104
|
|
|
-5.9 103
|
|
3.89 104
|
|
5.99 105
|
6.15 104
|
|
Qz1
|
|
|
1.77 104
|
|
-1.8 106
|
|
|
|
|
|
-1.8 104
|
|
-1.8 106
|
|
|
|
Mx1
|
|
-3. 9 104
|
|
7.37 105
|
|
-3.9 106
|
3.73 107
|
|
|
3.89 104
|
|
-7.4 105
|
|
-3.9 106
|
3.73 107
|
|
My1
|
3.44 103
|
|
-1.8 106
|
|
2.54 108
|
|
|
|
-3.4 103
|
|
1.77 106
|
|
9.99 107
|
|
|
|
Mz1
|
|
5.99 105
|
|
-3.9 106
|
|
8.07 107
|
6.32 106
|
|
|
-5.9 105
|
|
3.89 106
|
|
3.91 107
|
5.98 106
|
|
B1
|
|
6.15 104
|
|
3.73 107
|
|
6.32 106
|
5.30 109
|
|
|
-6.1 104
|
|
-3.7 107
|
|
5.98 106
|
2.24 109
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2
|
-6.9 105
|
|
|
|
-3.4 103
|
|
|
|
6.98 105
|
|
|
|
3.44 103
|
|
|
|
Qz2
|
|
-5.9 103
|
|
3.89 104
|
|
-5.9 105
|
-6.1 104
|
|
|
5.99 103
|
|
-3. 9 104
|
|
-5.9 105
|
-6.15 104
|
|
Qz2
|
|
|
-1.8 104
|
|
1.77 106
|
|
|
|
|
|
1.77 104
|
|
1.77 106
|
|
|
|
Mx2
|
|
3.89 104
|
|
-7.4 105
|
|
3.89 106
|
-3.7 107
|
|
|
-3. 9 104
|
|
7.37 105
|
|
3.89 106
|
-3.73 107
|
|
My2
|
-3.4 103
|
|
-1.8 106
|
|
9.99 107
|
|
|
|
3.44 103
|
|
1.77 106
|
|
2.54 108
|
|
|
|
Mz2
|
|
5.99 105
|
|
-3.9 106
|
|
3.91 107
|
5.98 106
|
|
|
-5.9 105
|
|
3.89 106
|
|
8.07 107
|
6.32 106
|
|
B2
|
|
6.15 104
|
|
3.73 107
|
|
5.98 106
|
2.24 109
|
|
|
-6.1 104
|
|
-3.7 107
|
|
6.32 106
|
5.30 109
|
В
таблице 3 жирной рамкой обведены коэффициенты, происхождение которых не совсем
понятно. Они имеют вполне значимые величины, которые нельзя отнести к
погрешностям расчета. Эти коэффициенты соответствуют появлению бимомента от
единичного смещения опоры вдоль оси Y и от поворота
опоры вокруг оси Z. И,
симметрично, - возникновению реакций в связи в направлении оси Y и
момента в связи, препятствующей вращению вокруг оси Z от
наложения на узел единичной депланации. На рис.4 показаны эпюры депланации и
бимомента балки от единичного смещения левого конца вдоль оси Y (a. и b.) и от
единичного поворота левого конца вокруг оси Z (c. и d.).
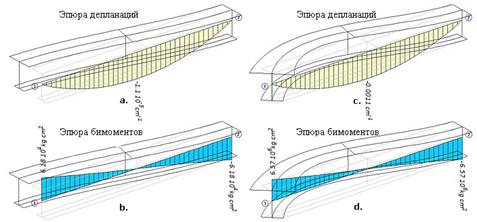
Рис.4
Для построения
эпюр на базе программы Selena [6] был разработан
специальный блок, позволяющий в автоматическом режиме строить сечения
конечноэлементных моделей балок, вычислять все геометрические характеристики
сечений и путем численного интегрирования вычислять интегралы вида
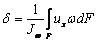 и
и 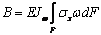 ,
,
где d и B –депланация
и бимомент, ux –
продольные перемещения точек сечения, sx –
продольные напряжения в сечении, Jw – секториальный
момент инерции сечения [2]. Обращает на себя внимание два момента – во-первых
абсолютное сходство эпюр депланации по форме (независимо от внешнего
воздействия) и, если предположить, что эпюры депланации описываются параболами,
то эпюры бимоментов точно соответствуют соотношению
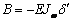 .
.
Странность этих
эпюр состоит в том, что депланация – это, как известно, первая производная от
угла закручивания стержня. Но при данных видах деформации никакого закручивания
не происходит. Мы рискнем предположить, что причиной возникновения этой "странной"
депланации являются деформации сдвига, возникающие в поясах двутавра. Как было показано
выше, перемещения балки с учетом деформации сдвига от действия поперечной силы,
определяется выражением (3). Соответствующий им угол поворота определяется
выражением
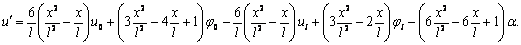 (12)
(12)
Применим эту
формулу к каждому из составляющих сечение элементов – нижней полке, верхней
полке и стенке двутавра. Очевидно, поворот, описываемый первыми четырьмя
членами этой формулы, будет совершенно одинаковым для всех упомянутых выше
элементов. А вот поворот, описываемый последним пятым членом, для верхней и
нижней полок будет различным. Поскольку нас интересует деформация,
ответственная за продольные напряжения, из этого выражения надо вычесть “чистый” сдвиг α. На рис.5а
показано распределение усилий между полками сечения
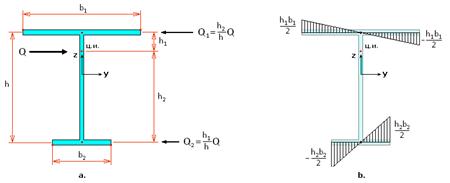
Рис.5
Поскольку при смещении сечение не
закручивается, равнодействующая перерезывающей силы приложена к центру изгиба.
Дополнительный поворот верхнего и нижнего поясов определяется выражением

Для прямоугольного сечения (имеются в виду сечения
полок)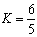 . Подставляя
сюда выражения для Q1 и Q2 (см.
рис.5а), получаем
. Подставляя
сюда выражения для Q1 и Q2 (см.
рис.5а), получаем

Нормальное
перемещение точек сечения задается выражениями
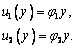
Депланация
сечения равна
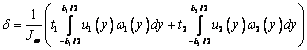 (13)
(13)
Здесь ω1(y) и ω2(y) – эпюра
ω на верхней и нижней полках соответственно (эпюра
секториальных площадей показана на рис.5b). Делая в
последнее выражение соответствующие подстановки, после несложных
преобразований, получаем
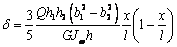 .
.
Или, в точке максимума
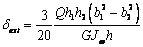 .
.
В случае
единичного сдвига вдоль оси Y – Q=5989 кг (см. табл.1,
реакция Qy от
смещения вдоль оси Y). Имеем
(G=8.077∙105
кг/см2, Jw=1.153∙105
см6)
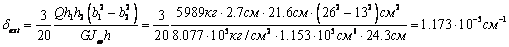
Аналогично, для случая единичного поворота вокруг
оси Z имеем: Q=5.99∙105кг (см. табл.1,
реакция Qy от
поворота вокруг оси Z) и d=1.173∙10-3см-1. Эти
значения почти точно совпадают с результатом численного эксперимента –
соответственно dY=1.10∙10-5см-1
и
dφz=1.10∙10-3см-1 (см.
рис.4). Таким образом, на основе полученных результатов можно утверждать с
достаточной степенью уверенности, что в основе возникновения такой “странной” депланации
без закручивания лежит различие во влиянии сдвиговых деформаций на различные
элементы сечения. Об этом свидетельствуют совпадение и численного значения с
экспериментом и формы кривой. Очевидно, что проявляется этот эффект только для
несимметричных сечений. Для симметричных сечений данный эффект отсутствует.
Теперь осталось
обобщить полученный результат на произвольные сечения. Прямую подсказку дает
формула (13). Пусть, например, в результате перемещений концов стержня в нем
возникла перерезывающая сила Qy и мы можем
построить эпюру касательных напряжений в сечении ty (здесь,
как и раньше нижний индекс ‘y’ говорит о том, что система напряжений
строится от силы, действующей в направлении оси Y; сами
же касательные напряжения действуют вдоль соответствующих сегментов сечения).
При наличии перерезывающей силы каждое сечение балки получает дополнительный
поворот
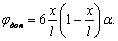 (14)
(14)
(см. формулу (12)),
где α – угол
чистого сдвига, вызванного действием перерезывающей силы. При этом, из-за
разного сопротивления сдвигу, угол α для различных
сегментов сечения может быть неодинаковый, что приводит к искажению сечения.
Деформация сечения из его плоскости от чистого сдвига определяется выражением (7).
Будем
предполагать,
что искажение формы сечения близко к закону секториальных площадей, т.е. 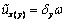 и
и 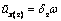 . Подберем
коэффициенты dy и dz так,
чтобы эти поверхности наименее отклонялись от функций ux(y) и ux(z) в
смысле наименьших квадратов. Имеем
. Подберем
коэффициенты dy и dz так,
чтобы эти поверхности наименее отклонялись от функций ux(y) и ux(z) в
смысле наименьших квадратов. Имеем
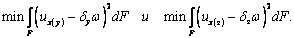
Откуда
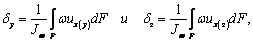
где Jw – секториальный
момент инерции сечения. Вводя подобно (9) характеристики
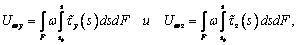
имеем
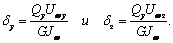
Очевидно, параметры dy
и
dz являются
аналогами αy и αz (10). По
аналогии с (11) введем коэффициенты депланации от сдвига Kwy
и
Kwz:
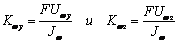
(коэффициенты Kwy и Kwz имеют размерность обратную
единицам длины). Тогда депланация будет представлена следующим образом
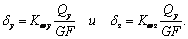
Физический смысл
характеристик Uwy и Uwz – секториальный статический
момент нормальных перемещений сечения от касательных напряжений, вызванных
действием единичных перерезывающих сил в направлении осей, соответственно, Y и Z.
Заметим также, если сечение обладает симметирией относительно оси Y, то Kwz=0 и, аналогично,
при симметрии относительно оси Z, то Kwy=0.
Теперь, в соответствии с (14) надо заменить φ на d, а α – на 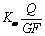 . Таким
образом, депланайия, будет определена зависимостями
. Таким
образом, депланайия, будет определена зависимостями
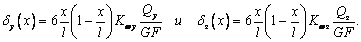 (15)
(15)
Депланация
в середине балки

А
бимоменты на концах стержня найдем из выражения 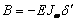 :
:
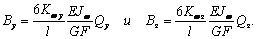
Литература
- Биргер И.А., Мавлютов Р.Р., Сопротивление материалов. - М. Наука, 1986, - 560 с.
- Бритвин Е.И., К расчету рамных конструкций, составленных из тонкостенных стержневых элементов.
- Власов В.З., Тонкостенные упругие стержни / М.: Физматгиз, 1959, - 574 с.
- Городецкий А.С., Здоренко В.С., Карпиловский В.С., Применение МКЭ к расчету тонкостенных стержневых систем // Сопротивление материалов и расчет сооружений. Вып. 28. – Издательство Будивэльнык, 1976. – С. 134-140.
- Перельмутер А.В., Юрченко В.В., К вопросу расчета пространственных конструкций из тонкостенных стержней открытого профиля. – Сборник научных работ УкрНИИПСК. – Выпуск 13, 2014. – С.12-26.
- Прочность, устойчивость, колебания. Универсальный программный комплекс для расчета конструкций на прочность. SELENA. 389 c.