|
3.2.4. Проверка устойчивости стержневых конструкций
Согласно сложившемуся в настоящее время представлению о природе потери устойчивости стержневых
систем, причиной того, что стержневые элементы конструкций теряют устойчивость при продольных усилиях
меньших, чем это предсказывает теория Эйлера, является наличие малых начальных случайных искривлений и
эксцентриситетов при прикреплении стержней. Поэтому, даже если стержень центрально сжат, в нем возникают
изгибающие моменты и, если фибровые напряжения в какой-то момент превышают предел текучести материала,
процесс потери устойчивости начинает развиваться с катастрофической скоростью. Если предположить, что
начальное искривление меняется по синусоидальному закону, нетрудно получить формулу для предельного значения
сжимающей силы, при которой в крайней фибре стержня появляется расчетное напряжение Ry
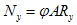 (1) (1)
где A – площадь поперечного сечения стержня, а j – коэффициент, вычисляемый по формуле
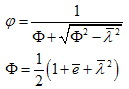 (2) (2)
где
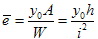 - относительный начальный эксцентриситет и
- относительный начальный эксцентриситет и
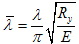 - приведенная гибкость стержня, y0 – стрела погиби стержня, W – момент сопротивления сечения.
- приведенная гибкость стержня, y0 – стрела погиби стержня, W – момент сопротивления сечения.
Таким образом, если бы был известен предельный начальный эксцентриситет стержня, по формуле (1) можно
было бы вычислить предельное значение продольной силы, непревышение которой гарантирует отсутствие пластических
деформаций. В европейских (Eurocode 3), американских, израильских и других нормах для вычисления коэффициента
j используется непосредственно формула (2). Разница состоит только в
нормировании эксцентриситета.
Как правило, принимается линейная зависимость эксцентриситета от гибкости
где коэффициент a зависит от типа сечения и расчетного сопротивления.
В российских нормах (СНиП II-23-81) нормируется непосредственно коэффициент j:
где
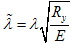 .
.
Однако, насколько бы ни была сложная зависимость
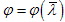 , всегда можно, обратив формулу (2), получить зависимость для
, всегда можно, обратив формулу (2), получить зависимость для
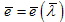
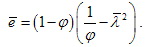 (3) (3)
Этот факт дает возможность проверить устойчивость стержневой конструкции следующим образом – введем в
стержни погиби, амплитуды которых определены формулой (3), и рассчитаем конструкцию по деформированной
схеме (расчет по деформированной схеме необходим, поскольку величина погиби существенно зависит от продольной силы).
Стержни можно включить в конструкцию двумя способами: сопрягая углы поворота стержней в узлах (такая форма
соединения стержней характерна, например, для соединений на болтах) и не сопрягая углы поворота (такая форма
включения стержней, скорее всего, будет свойственна для сварных соединений). Включение стержней по схеме с
сопряжением углов поворота можно представить следующим образом: на узлы конструкции накладываются связи,
препятствующие поворотам; перед присоединением каждый стержень выгибается так, чтобы все его точки лежали
на прямой линии – в таком виде стержень монтируется в систему; после того, как вся система смонтирована,
убираются лишние связи, наложенные на узлы. Основная проблема при этом состоит в задании направлений погибей
для различных стержней. В программе эта проблема решается следующим образом:
-
строится форма потери устойчивости конструкции (линейный расчет);
-
направления погибей стержней выбираются таким образом, чтобы при включении стержней по схеме с “сопряжением
углов поворота”, работа сопрягающих моментов на перемещениях формы потери устойчивости была наибольшей.
Построенная таким образом конфигурация погибей не гарантирует наихудшее с точки зрения напряжений состояние
конструкции. Поэтому программа делает еще один расчет по деформированной схеме с обратным направлением погибей
по отношению к определенным на предыдущей стадии. Затем программа выполняет серию расчетов по деформированной
схеме (число расчетов определяет пользователь), генерируя знаки и значения амплитуд погибей случайным образом.
Величина погиби (эксцентриситета) формируется как случайная величина, распределенная по нормальному закону в
интервале [0,X] (X – предельное значение погиби или эксцентриситета, определяемые в соответствии с изложенной
выше методикой для каждого стержня в отдельности) с центром в точке X/2 и стандартом X/5 (величина стандарта
X/5 выбрана произвольно – исследования показали, что результат мало зависит от величины стандарта). В результате
для сформированной выборки программа вычисляет для каждого стержня математическое ожидание (среднее значение
по выборке) напряжения от продольной силы, математические ожидания и стандарты отклонения верхнего и нижнего
фибровых напряжений, максимальные и минимальные значения верхнего и нижнего фибровых напряжений. В программе
также предусмотрен режим, позволяющий получить верхние и нижние фибровые напряжений в стержнях с вероятностью
превышения 95%, 99% и 99.9%.
|