3.2.1. Линейный расчет

Основной задачей расчета на устойчивость является определение значения критического параметра потери устойчивости конструкции - k (физический смысл критического параметра потери устойчивости состоит в том, что если увеличить нагрузки, действующие на конструкцию в k раз, то система потеряет устойчивость).

Перед началом расчета программа запрашивает относительную точность поиска критического значения

и расчетную комбинацию статических загружений, на которую будет произведен расчет

Никаких дополнительных таблиц для расчета на устойчивость заполнять не надо.

Расчет инициируется вызовом пункта меню

Расчет выполняется последовательными итерациями. В качестве нагрузки задается некоторая расчетная комбинация статических загружений (если ранее статический расчет не выполнялся, то он выполняется автоматически). На каждой итерации продольные усилия в стержневых элементах и напряжения в срединной поверхности оболочечных элементов, взятые из расчетной комбинации загружений, умножаются на некоторый пробный множитель k и матрица единичных реакций системы формируется с учетом полученного продольного напряженного состояния в конечных элементах. Вычисляется степень неустойчивости системы n - число пройденных собственных значений системы. Если n=0, то k изменяется в сторону увеличения. Если n>0, то k изменяется в сторону уменьшения (в программе реализован метод деления отрезка пополам). Процесс вычисления продолжается до тех пор, пока не будет достигнута некоторая заданная относительная точность определения числа k.

Результатом расчета на устойчивость являются значение критического параметра потери устойчивости, форма потери устойчивости, а также для стержневых элементов значения гибкостей, коэффициентов свободной длины и расчетные длины.

При использовании расчетных длин элементов, необходимых для некоторых СНиПовских проверок пользователь должен проявлять известную осторожность. Достоверные значения расчетных длин, гибкостей будут выданы только для наиболее нагруженных (ответственных за потерю устойчивости) стержней. Для того чтобы установить, какие стержни ответственны за потерю устойчивости, достаточно построить форму потери устойчивости - наиболее "выпучившие" и есть искомые стержни. Для всех остальных стержней при определении расчетных длин следует воспользоваться рекомендациями СНиП (заметим, что это происходит с мало нагруженными стержнями и, поэтому, точность при определении расчетных длин таких стержней, как правило, мало существенна).

Точность построения формы потери устойчивости зависит от точности поиска критического значения k. Во-первых, может оказаться, что между наибольшим значением k, находящимся левее первого собственного значения и наименьшим значением k, расположенным правее первого собственного значения, находится более одного собственного значения. В этом случае построение формы потери устойчивости вообще невозможно. Такая ситуация наиболее типична для оболочек.

Важнейшим критерием потери устойчивости системы является изменение знака последнего диагональным элементом матрицы жесткости с плюса на минус. Характер изменения последнего диагонального коэффициента несет в себе важнейшую информацию о характере потери устойчивости системы. Поэтому остановимся на некоторых нюансах поведения системы при прохождении через собственное значение.

Как уже было сказано ранее, при прохождении системы через собственное значение последний диагональный элемент матрицы жесткости проходит через ноль. Далее график устремляется к минус бесконечности (разрыв второго рода). Однако сказанное выше может быть несправедливо для систем с вырожденными и разделяющимися формами потери устойчивости. В этом случае единственным критерием прохождения системы через критическое значение может служить число пройденных собственных значений. Сложности могут также возникнуть при наличии очень слабых элементов в системе ("почти вырожденные формы"). В этом случае бывает трудно поймать момент перехода последнего диагонального элемента через ноль. Те же трудности возникают при очень густом спектре собственных значений.

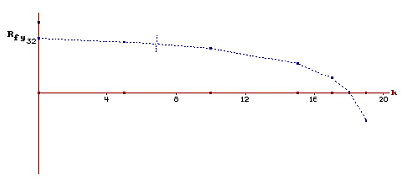
На рисунке ниже показан типичный пример поведения последнего диагонального элемента для "хорошей" системы.

Совершенно другая картина может возникнуть при анализе систем со "слабыми" элементами. Под словом "слабые" здесь понимается достаточно гибкие обжатые стержни. Программа всегда ищет общую форму потери устойчивости. И если узел, которому соответствует последний диагональный элемент, находится достаточно далеко от места, где расположены "слабые" элементы, система может "не почувствовать" потерю устойчивости "слабыми" элементами. График изменения последнего диагонального элемента останется практически без изменений и только при более детальном рассмотрении в месте, где действительно произошла потеря устойчивости, можно будет обнаружить очень резкий разрыв второго рода.

Точность построения формы потери устойчивости зависит от того, насколько близко график изменения последнего диагонального элемента подошел к нулю. Поэтому, иногда для достоверного построения формы потери устойчивости приходится увеличивать точность поиска критического значения до тысячных и более долей. В случае вырожденных форм потери устойчивости (например, устойчивость теряет шарнирно опертый стержень, включенный в систему), форму потери устойчивости вообще построить невозможно.

Поскольку программа выдает график изменения последнего и предпоследнего диагонального элемента, у пользователя всегда есть возможность проконтролировать качество построения формы потери устойчивости.