|
3.19. Особенности расчета конструкций, содержащих элементы предварительно напряженных тяг
Предварительно напряженный элемент тяги подобен вантовому конечному элементу. Как правило, это и есть канат, натягиваемый или при помощи талрепов или на специально фиксируемые упоры. Главное отличие тяги от ванта – натяжение должно быть таким, чтобы обеспечить линейную работу элемента. Еще одно важное отличие тяги от каната – тяга может объединять сразу несколько узлов. Элемент тяги всегда натягивается “на конструкцию” и жестко крепится к ней своими крайними узлами. Ко всем промежуточным узлам тяга крепится со скольжением, что обеспечивает одинаковую силу натяжения во всех сегментах тяги. Общее число узлов, объединяемых одной тягой должно быть не более 12. Примеры использования элемента тяги см. п. Предварительно напряженный элемент тяги.
Натяжение тяги задается как рядовая местная нагрузка (см. пп. Статические местные нагрузки, Нагрузки, прикладываемые к предварительно напряженному элементу тяги). Обязательное условие – натяжение должно соответствовать напряженному состоянию первого загружения и, соответственно, натяжение может быть задано только в рамках первого загружения. Если натяжение задать со знаком ‘-‘, то такая тяга будет моделировать работу домкрата. В этом случае тяга должна состоять из одного сегмента. Еще, в качестве нагрузки к элементу тяги может быть приложен температурный нагрев. Температурный нагрев может быть приложен во всех загружениях, начиная со второго. Т.е. температура задается относительно первого загружения.
Свойства тяги характеризуются жесткостью EA. Если тяга состоит из нескольких элементов, например, талрепа и каната, то следует вводить приведенную жесткость – 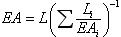 . Если прикладывается температурная нагрузка, то также необходимо задать коэффициент линейного расширения a. Если заданы ветровая или гололедная нагрузки, то должен быть задан диаметр тяги. Если задан погонный вес тяги, то собственный вес тяги учитывается автоматически в первом загружении. . Если прикладывается температурная нагрузка, то также необходимо задать коэффициент линейного расширения a. Если заданы ветровая или гололедная нагрузки, то должен быть задан диаметр тяги. Если задан погонный вес тяги, то собственный вес тяги учитывается автоматически в первом загружении.
Если конструкция, в которой используются элементы тяги, не содержит нелинейно работающих элементов вант, результаты в режиме статического расчета по первому загружению будут соответствовать нагрузкам первого загружения. По всем остальным загружениям результаты следует интерпретировать как добавки к первому заружению. При этом можно вводить любые коэффициенты к результатам по всем загружениям старше первого при добавлении их к результатам первого загружения. Таким образом, если в конструкциях без элементов тяги каждое загружение имеет самостоятельное значение, то при наличии тяг все загружения старше первого должны интерпретироваться совместно с первым загружением. Если конструкция наряду с элементами тяг содержит вантовые элементы, то здесь вступает правило обработки вантовых конструкций (см. п. Расчет вантовых конструкций) - по каждому из загружений результат выдается от комбинации нагрузок первого и соответствующего загружения.
Расчетная схема не может одновременно с элементами тяг содержать нелинейные элементы np, nd, nt, rl (см. п.Конечные элементы). Также, при наличии элементов тяг, не может быть выполнен расчет Регулировка натяжения вант. В последнем случае рекомендуется просто заменить элементы тяг вантовыми элементами.
Если элемент тяги имеет внутренние узлы, к которым не крепятся никакие другие упругие элементы, то все эти узлы должны располагаться на прямой линии, соединяющей начало и конец тяги и силы, приложенные к внутренним узлам не должны иметь проекцию на ось тяги. Заметим, что будет неправильно прикладывать поперечные силы к внутренним узлам такой тяги в загружениях старше первого, поскольку перемещения этих узлов зависят от полного натяжения тяги, которое заранее не известно. В такой ситуации следует прибегнуть к расчету по Деформированной схеме. В этом случае натяжение канатов будет учтено корректно.
Если задан погонный вес тяги, то при динамических расчетах масса тяги учитывается автоматически.
В каких случаях целесообразно или нецелесообразно использовать элемент предварительно напряженной тяги? Рассмотрим следующий пример. Пусть в нашем распоряжении имеется консольный стержень, изображенный на рис.А. Сам стержень невесомый, а на его конце прикреплена масса m.
Частота собственных колебаний такого стержня равна 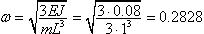 . А критическая сила - . А критическая сила - 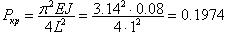 . Введем в схему предварительно напряженную тягу (рис.B), соединив ею основание и вершину стержня. Выполнив по программе расчет на собственные колебания и устойчивость, получим следующие значения: w = 0.2703 и Pкр = 0.1773 (для расчета устойчивости начальное значение внешней сжимающей силы было принято равнм 0.1). Этот результат вполне предсказуем: реакция стержня от единичного горизонтального смещения его верха равна . Введем в схему предварительно напряженную тягу (рис.B), соединив ею основание и вершину стержня. Выполнив по программе расчет на собственные колебания и устойчивость, получим следующие значения: w = 0.2703 и Pкр = 0.1773 (для расчета устойчивости начальное значение внешней сжимающей силы было принято равнм 0.1). Этот результат вполне предсказуем: реакция стержня от единичного горизонтального смещения его верха равна
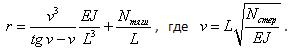
Для свободных колебаний Nстер = Nтяги = N, и частота колебаний - 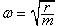 . Подстановка численных значений в эти формулы дает - w = 0.2703. Для устойчивости . Подстановка численных значений в эти формулы дает - w = 0.2703. Для устойчивости 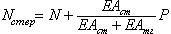 и и 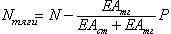 , где P – сжимающая сила, приложенная к вершине стержня. А критическое значение силы P находится из условия r(P) = 0. Решая это уравнение, находим Pкр = 0.1904. Как видно, значение частоты совпало точно, а значение критической силы несколько отличается. Расхождение в критической силе связано с тем, что при поиске критического параметра программа вместе с внешней нагрузкой меняет и натяжение тяги. Поэтому результат расчета по программе будет зависеть от величины внешней нагрузки. Т.е. для программы выражения для Nстер и Nтяги выглядят несколько иначе - , где P – сжимающая сила, приложенная к вершине стержня. А критическое значение силы P находится из условия r(P) = 0. Решая это уравнение, находим Pкр = 0.1904. Как видно, значение частоты совпало точно, а значение критической силы несколько отличается. Расхождение в критической силе связано с тем, что при поиске критического параметра программа вместе с внешней нагрузкой меняет и натяжение тяги. Поэтому результат расчета по программе будет зависеть от величины внешней нагрузки. Т.е. для программы выражения для Nстер и Nтяги выглядят несколько иначе - 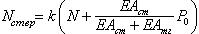 и и 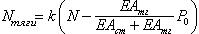 , где k – критический параметр. В нашем случае мы задались значением Po = 0.1 и получили значение k = 1.773 (т.е. Pкр = 0.1*1.773 = 0.1773). Если, например, взять Po = 0.2 (что очень близко к искомому значению критической силы), то в результате расчета получим Pкр = 0.1930. Иными словами, чем лучше мы угадаем начальные значения сил, тем точнее будет результат. , где k – критический параметр. В нашем случае мы задались значением Po = 0.1 и получили значение k = 1.773 (т.е. Pкр = 0.1*1.773 = 0.1773). Если, например, взять Po = 0.2 (что очень близко к искомому значению критической силы), то в результате расчета получим Pкр = 0.1930. Иными словами, чем лучше мы угадаем начальные значения сил, тем точнее будет результат.
Слегка изменим расчетную схему, разделив наш стержень на 10 участков длиной по 0.1 каждый. А двухточечную тягу заменим тягой, состоящей из 10-и участков. Крайние узлы тяги, как и раньше, крепятся к основанию и вершине стержня, а внутренние узлы примыкают к соответствующим узлам стержня, не давая тяге возможности отделится от него при поперечных перемещениях, но свободно проскальзывающих в продольном направлении (рис.С). Рассчитаем по программе собственную частоту и критическую силу такой конструкции. Вычисления дают следующие значения: w = 0.2827 и Pкр = 0.1973. Как видно, частота и критическая сила практически точно совпадают с соответствующими значениями стержня без тяги. Даже при увеличении предварительного натяжения в 10 раз, мы получаем следующие значения для параметров: w = 0.2814 и Pкр = 0.1913. Т.е., мы видим, что собственная частота колебаний и критическая сила для такого стержня фактически не зависит от начального натяжения тяги. У этого феномена есть простое объяснение. Запишем уравнение изгиба балки, сжатой силой N:
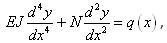
где q(x) – распределенная нагрузка на балку. Распределенная нагрузка слагается из двух составляющих – собственно внешней нагрузки на балку qo(x) и давления со стороны растянутой тяги на стержень, возникающего из-за искривления оси стержня. Это давление выражается простой формулой 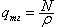 , где r - радиус кривизны изгиба стержня. Учитывая, что , где r - радиус кривизны изгиба стержня. Учитывая, что 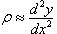 , уравнение изгиба такого стержня приобретает стандартный вид , уравнение изгиба такого стержня приобретает стандартный вид
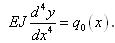
Т.е. предварительное натяжение отдельных элементов не меняет их динамические и критические параметры. Как не натягивай арматуру, железобетонный стержень от этого не потеряет устойчивость (при условии, что арматура соприкасается с телом стержня). Поэтому, если у вас есть необходимость учесть предварительное натяжение отдельных элементов конструкции, то не стоит моделировать натяжение арматуры при помощи системы тяг. Проще посчитать приведенные характеристики стержня с учетом арматуры (площадь, момент инерции) и включить его в качестве обычного стержня в расчет. По окончанию расчета к напряженному состоянию тела стержня и арматуры надо добавить напряжения от собственного предварительного натяжения арматуры.
Рассмотрим еще один элементарный пример. Пусть к вершине нашего консольного стержня приложена горизонтальная сила P = 1. Горизонтальное перемещение вершины консоли без предварительно напряженной тяги (схема А) составляет 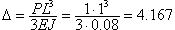 . Для схемы В перемещение найдем по формуле . Для схемы В перемещение найдем по формуле 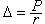 , где r - реакция стержня от единичного горизонтального смещения его верха при условии Nстер = Nтяги = N. Прямое вычисление дает D = 4.5611. В то же время обычный статический расчет по программе дает значение того же перемещения D = 2.9412. Такой же статический расчет по схеме С дает значение перемещения D = 2.7849. И это в то время, как мы пришли к заключению, что предварительное натяжение не должно влиять на жесткость стержня. , где r - реакция стержня от единичного горизонтального смещения его верха при условии Nстер = Nтяги = N. Прямое вычисление дает D = 4.5611. В то же время обычный статический расчет по программе дает значение того же перемещения D = 2.9412. Такой же статический расчет по схеме С дает значение перемещения D = 2.7849. И это в то время, как мы пришли к заключению, что предварительное натяжение не должно влиять на жесткость стержня.
Проблема здесь состоит в том, что мы не учли, что обычный статический расчет выполняется в предположении, что отсутствуют продольные силы в стержнях. Если выполнить расчет по Деформированной схеме, то все станет на свои места, поскольку этот расчет учитывает продольное напряженное состояние элементов. Для схемы В по деформированной схеме получаем D = 4.5611 а по схеме С - D = 4.1710 что все ставит на свои места. Такое сильное расхождение между двумя расчетами объясняется тем, что заданное предварительное натяжение тяги N = 0.1 не очень далеко от критической силы стержня (напомним, Pкр = 0.1974). Как видно, наша забывчивость в некоторых случаях может привести к очень печальным результатам. Этот пример лишний раз подчеркивает, что не стоит городить лес там, где этого не надо делать. Моделировать предварительное натяжение арматуры в бетоне при помощи тяг - не лучшее решение. Для этого в вашем распоряжении есть возможность прямого учета предварительного натяжения арматуры в бетоне - Расчет конструкций из предварительно напряженного железобетона.
|