3.23. Вибромониториг

В инженерной практике часто возникает задача – дать оценку работоспособности конструкции, на которой установлена некоторая производственная линия, включающая вращающиеся элементы: роторы моторов, валы, барабаны и т.п. Следствием работы таких элементов является повышенная вибрация сооружения, что в некоторых случаях даже может привести к его разрушению. Причина возникновения вибрации – малые эксцентриситеты вращающихся элементов. Просто расставить в определенных местах датчики ускорений и снять акселерограммы, не решает проблему. Задача состоит в том, чтобы построить адекватную расчетную схему возбуждения конструкции, а без знания возмущающих усилий эту задачу решить невозможно. Возмущающими силами в данном случае, понятно, являются центробежные силы инерции, вычисляемые по формуле F=mw²D, где m – масса вращающегося элемента, w – частота вращения и D – эксцентриситет массы относительно оси вращения. Как правило, параметры m и w для каждого вращающегося элемента известны. А с эксцентриситетом D, - проблема. Мало того, что практически нет никакой возможности померить его “вручную”, он еще и имеет тенденцию меняться во времени.

Также, часто, кроме того, что необходимо дать оценку текущему состоянию конструкции, заказчик ставит перед инженерами задачу оценить возможность увеличения производительности оборудования, что означает увеличение частот вращения валов, барабанов и всего прочего оборудования. А эту задачу уж точно не решишь без построения адекватной модели. В данном разделе мы опишем процедуру решения данной задачи средствами программы Selena.

Ниже на рисунке представлена схема рамной конструкции.

На ригелях рамы установлено оборудование, которое моделируется сосредоточенными массами, расположенными в уровне ригелей. В центре каждого пролета в точках A, B и C установлены моторы, угловая скорость вращения роторов которых составляет соответственно 40, 45 и 50 рад/с. Четыре нижние собственные частоты колебаний конструкции составляют: 26.42, 42.85, 48.04 и 54.89 рад/c. Ниже показаны формы собственных колебаний конструкции.

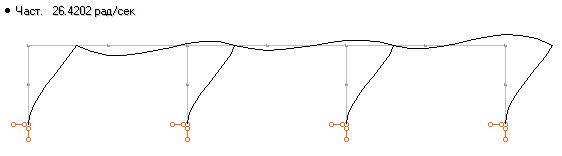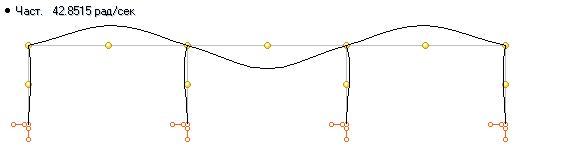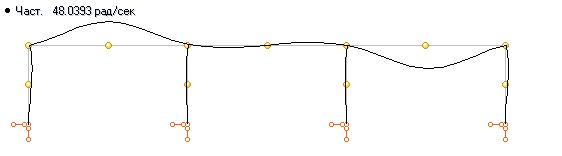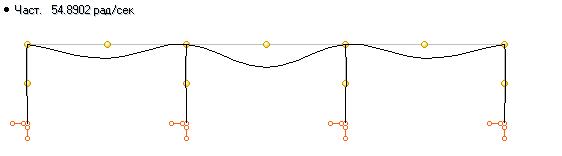
Выбираем точку, в которой установим датчик ускорений. Эта точка должна иметь заметные перемещения от всех вибрационных нагрузок. В нашем случае удобно выбрать точку А. Ускорения будем мерить в вертикальном направлении. Точка установки датчика совсем не обязательно должна совпадать с местом приложения одной из вибрационных нагрузок. Единственное требование к положению датчика и направлению его действия – перемещения от всех возмущающих нагрузок в этом месте и в этом направлении должны быть существенными. Далее, включаем оборудование, дожидаемся, когда затухнут собственные колебания и снимаем акселерограмму. Акселерограмма должна быть оцифрована в формате Standard for the Exchange of Earthquake Data (Спектральный анализ). Входим а режим Спектральный анализ

и загружаем акселерограмму

Программа тут же выдает спектрограмму процесса

Как видно, спектр несколько размазан. “Качество” построения спектра зависит от количества снятых отсчетов и от кратности шага снятия отсчетов периоду колебаний каждой из гармоник. Чтобы найти действительные значения частот и амплитуд каждой из гармоник, щелкаем по пиктограмме на панели инструментов. Программа приводит “расплывшийся” спектр к линейчатому и в табличной форме выдает значения частот и амплитуд

Переходим от амплитуд ускорений к амплитудам перемещений по формуле d=a/w². Получаем: D₁=5.716 10^-3 м, D₂=8.969 10^-3 м, D₃=2.339 10^-3 м (нижний индекс обозначает номер частоты возмущения).

Входим в Графический редактор и в режиме НАГРУЗКИ/ГАРМОН.ДИН. (гармоническое динамическое воздействие). Выбираем тип нагрузки – гармоническое возбуждение центробежной силой от вращающейся массы

и создаем 3 загружения (по числу моторов) с единичной нагрузкой

и тремя различными частотами вращения: w₁=40 c^-1, w₂=45 c^-1 и w₃=50 c^-1.

(“единичная” нагрузка me=1 автоматически умножается на квадрат частоты вращения массы; поэтому подписываемое под нагрузкой значение силы фактически равно mew²). Выполняем расчет на Вынужденные гармонические колебания

и снимаем показания расчета в контрольной точке А по каждому их трех загружений:

Нас интересует вертикальное перемещение. Расчет на Вынужденные гармонические колебания выполняется в комплексной моде. Поэтому значения по каждой переменной выдается в виде суммы u=a+ib. Комплексную компоненту каждого числа следует интерпретировать как гармоническое колебание со сдвигом по фазе на 90^o. Т.е. на самом деле u=a sin(wt)+b sin(wt). Но нас интересует амплитуда перемещений.

(нижний буквенный индекс обозначает номер мотора, от которого вычисляются перемещения в контрольной точке). Размерность кг^-1 связана с тем, что перемещения d вычислены от единичного значения произведения me, которое имеет размерность кг*м. Таким образом, произведение med имеет размерность м. Обозначим для краткости искомые величины (me)_A=x_A, (me)_B=x_B, (me)_C=x_C. Тогда, очевидно, справедливы равенства

Из этих выражений находим

Если известны массы вращающихся деталей, то отсюда можно определить эксцентриситеты – e=x/m. Однако, в этом нет необходимости, поскольку для задания центробежной силы в программе все равно задается произведение m*e.

Приведенный выше пример сравнительно прост для вычислений, поскольку все три мотора имели разную частоту вращения. Ситуация несколько усложняется, если некоторые источники возмущения работают на одних и тех же частотах. В этом случае разделить колебания, вызываемые работой нескольких моторов на одной и той же частоте при помощи одного датчика невозможно. Выход состоит в том, чтобы поставить несколько датчиков. Т.е. минимально необходимое количество датчиков должно быть равно максимальному количеству моторов, работающих на одной и той же частоте. Покажем решение данной проблемы на примере все той же рамы с тремя моторами. Только будем считать, что моторы в точках A и B работают на одной и той же частоте 40 рад/с. При этом будем считать,, что нам известен сдвиг по фазе мотора В относительно мотора А составляет 45^o. Мотор в точке С, как и прежде, работает на частоте 50 рад/с. Выберем в качестве второй контрольной точки точку С. Чтобы не создавалась иллюзия, что контрольные точки должны совпадать с точками приложения нагрузки, будем снабжать измерения, относящиеся к контрольной точке А нижним индексом (1), а в точке С – индексом (2).

Ниже показана акселерограмма, записанная в точке А (датчик (1))

и ее е спектральное разложение

Щелчок по пиктограмме на панели инструментов дает

Переходя все по той же формуле d=a/w² от ускорений к перемещениям, получаем: D₁₍₁₎=9.378 10^-3 м, D₂₍₁₎=2.353 10^-3 м (первый индекс обозначает номер частоты возбуждения, второй в скобках – номер датчика).

Аналогично, в точке С (датчик (2)), получаем

В результате имеем: D₁₍₂₎=5.598 10^-3 м, D₂₍₂₎=2.662 10^-3 м.

Формируем 3 загружения с последовательным приложением “единичной” центробежной силы в точках A, B и C и с частотами возбуждения соответственно 40, 40 и 50 рад/с. И снимаем вертикальные перемещения в точках расположения датчиков (1) и (2). Имеем

Модули “единичных” перемещений

(здесь первый буквенный индекс – номер мотора (или, что то же) номер загружения, второй индекс в скобках – номер датчика). Составляем уравнения задачи. Поскольку на первой частоте 40 рад/с работают два мотора A и В, то их колебания складываются, что выражается в единой для них спектральной линии на частоте 40 рад/с на графике спектрального разложения. Однако складывать эти колебания надо с учетом их относительного сдвига по фазе, который мы договорились принять равным j_AB=45^o. Имеем

Решение этой нелинейной системы уравнений можно произвести, например, на Excel. Подстановка вычисленных ранее значений d_i(j) и D_k(j), дает: x_A=0.4649 кг м, x_В=0.5899 кг м. Для неизвестной x_C также имеем 2 уравнения:

Из первого из этих уравнений получаем x_C=0.1294 кг м, из второго - x_C=0.1288 кг м, что можно считать хорошим совпадением.

На практике, однако, вряд ли можно предположить, что нам заранее будет известен сдвиг по фазе моторов A и В. Выход становится очевидным, если взглянуть на нелинейную систему уравнений, которая позволила нам определить неизвестные x_A и x_B. Только величину j_AB нам надо рассматривать не как наперед заданную, а как неизвестную. Чтобы система с тремя неизвестными имела решение, в соответствии с основным правилом алгебры, мы должны иметь 3 условия.

Дополним нашу расчетную схему еще одним датчиком (3), который установим в точке В. Как и прежде будем мерить вертикальные перемещения. Ниже показана акселерограмма, записанная этим датчиком и ее спектральное разложение.

В результате приведения к линейчатому спектру, получаем.

и D₁₍₃₎=16.79/40.04²=10.4868 10^-3 м, D₂₍₃₎=2.57/49.96²=1.0287 10^-3 м (как и прежде, первый индекс – номер частоты, второй в скобках – номер датчика).

Модули вертикальных перемещений в точке расположения датчика (3) (точка В) от возмужения “единичными” центробежными силами, приложенными в точках А, В и С, составили

Формируем систему уравнений, для нахождения неизвестных x_A, x_B и j_AB. Имеем

Подстановка вычисленных ранее значений d_i(j) и D_k(j), дает: x_A=0.4538 кг м, x_B=0.5828 кг м и j_AB=39.05^o. Для неизвестной x_C также имеем 3 уравнения:

Из первого из этих уравнений получаем x_C=0.1294 кг м, из второго - x_C=0.1288 кг м, из третьего - x_C=0.1332 кг м, что также можно считать хорошим совпадением.

Как видно, во всех трех экспериментах мы получили практически одинаковые значения искомых неизвестных: x_A=0.4664 кг м, x_B=0.5914 кг м, x_C=0.1286 кг м. Понятно, что такое совпадение не случайно – для моделирования всех “экспериментальных” акселерограмм (именно они являлись основным источником информации) мы заложили в качестве исходных данных именно эти значения переменных. А угол сдвига по фазе между моторами A и B в экспериментах с совпадающими частотами, был принят равным 45 градусов. Как видно, если частоты вращения всех моторов различные, то нет никакой проблемы с определением параметров модели. Нам только осталось обобщить решение проблемы на случай совпадающих частот.

Пусть мы имеем систему с некоторым количеством моторов, работающих на K частотах. Выделим группу моторов G_k, работающих на k-й частоте. Обозначим количество моторов, принадлежащих группе G_k – N_k. Каждый из этих моторов имеет свой эксцентриситет вращения и, соответственно, имеем N_k параметров x_n (здесь n – номера моторов, относящихся к группе G_k). Кроме того, каждый из этих моторов вращается со своей фазой j_n. Нас, однако, интересуют не сами фазы, а их разности. Поэтому мы можем отнести все эти фазы к фазе, например, первого мотора в группе G_k. Таким образом, количество неизвестных фаз уменьшается на единицу. В результате для группы G_k имеем 2N_k-1 неизвестных. Следовательно, для определения параметров моторов, входящих в группу G_k нам надо установить как минимум 2N_k-1 датчиков. Поскольку одни и те же датчики могут использоваться для определения параметров моторов, относящихся к различным частотным группам, общее количество датчиков, необходимое для определения параметров всех моторов, равно 2N_k-1 для самой большой по количеству моторов частотной группе. В частности, если все моторы работают на разных частотах, то достаточно одного датчика. Может, конечно, случиться так, что датчиком, расположенном в одним месте невозможно уловить колебания от всех моторов. Тогда можно использовать несколько датчиков, расположенных в разных местах, увязывая их с моторами, дающими наиболее существенный вклад в их показания.

Итак, возвращаясь к группе G_k, работающей на k-й частоте. Мы имеем 2N_k-1 датчиков и, соответственно, снимаем 2N_k-1 акселерограмм. Делаем спектральное разложение для каждой акселерограммы и находим амплитуды ускорений по k-й частоте a_k(i) (i – номер датчика). Переходим от амплитуд к перемещениям D_k(i)= a_k(i)/w_k². Вычисляем амплитуды колебаний d_n(i) в точках расположения 2N_k-1 датчиков от “единичных” центробежных сил , приложенных в местах расположения моторов, принадлежащих группе G_k (здесь n - номер мотора, i – номер датчика). Формируем систему из 2N_k-1 уравнений

с 2N_k неизвестными x_n и j_n. Для замыкания системы уравнений одно из значений j_n надо положить равным нулю.