3.9.1. Почему комплексные числа?
Запишем уравнение гармонического осциллятора с вязким трением под действием гармонической силы
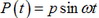
Будем искать его решение в виде
Подставляя это выражение в уравнение (1), получаем
Нетрудно убедиться в том, что в плоскости {u,P} пара уравнений
образуют эллипс. Площадь этого эллипса равна энергии Wd, рассеянной за один цикл движения.
Прямые вычисления дают
Разделив Wd на значение максимальной упругой энергии
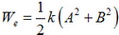 , получаем коэффициент поглощения энергии , получаем коэффициент поглощения энергии
Из последней зависимости следует, что с чем большей частотой возбуждать гармонический осциллятор, тем большая
энергия будет рассеиваться за один период колебаний. Такое рассеяние энергии называется частотно-зависимым.
Однако, хорошо известно, что большинство строительных материалов (сталь, железобетон) не обладают столь явно
выраженными реологическими свойствами. Так, например, основной причиной поглощения энергии в металлах является
их пластичность. Реальная кривая зависимости деформация – сила для металлов при циклическом нагружении имеет вид
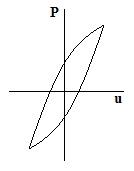
Форма и площадь этой петли (петли гистерезиса) зависят не только от свойств материала, но и от формы сечения
и вида напряженного состояния. Кроме того, в реальных конструкциях к поглощению энергии в материале добавляются
потери от трения в местах сочленения элементов конструкции. Все это делает практически невозможным точное
вычисление потерь для какой-либо реальной, даже небольшой, конструкции. С другой стороны, совершенно очевидно,
что не столь важна форма петли гистерезиса, сколько умение оценить ее площадь. Если нам откуда-то известна
эта площадь (например, из динамического эксперимента над целой конструкцией), можно построить достаточно
простые динамические уравнения, описывающие движение такой конструкции. Примером такого решения, как раз,
и является уравнение гармонического осциллятора с вязким трением. Главное достоинство этого уравнения –
его простота. Оно очень легко расширяется на системы со многими неизвестными и хорошо известно как его решать.
Единственным недостатком этого уравнения является выявленная выше зависимость потерь от внутреннего трения от
частоты возмущения.
Есть, однако, другой способ учета внутреннего трения. Хорошо известно, что если в уравнение гармонического
осциллятора ввести дополнительную силу сопротивления, пропорциональную смешению, но опережающую по фазе
возмущающую силу на 90 градусов, то движение такой системы в плоскости {u,P} также будет осуществляться по
эллиптической кривой. Действительно, в этом случае уравнение движения будет иметь вид
Здесь T - период вынужденных колебаний, а для силы трения введен коэффициент пропорциональности
gk, где k, как и раньше – жесткость пружины, а коэффициент
g называется “коэффициент внутреннего неупругого сопротивления”.
Будем, точно так же, как и в предыдущем случае искать решение этого уравнения в виде
Подставляя это выражение в уравнение (2), получаем
Точно так же вычислим коэффициент поглощения энергии
Как видно, в этом случае, поглощающие свойства осциллятора не зависят от частоты возмущения. Такое поглощение
энергии называется “сухим”.
Мы получили замечательный результат – трение стало частотно-независимым. Но в уравнение движения “вкрался”
странный член со “сдвигом по фазе”. Сделаем последний шаг к решению данной проблемы. Рассмотрим уравнение
Это уравнение отличается от уравнения гармонического осциллятора без сопротивления тем, что жесткость пружины
k умножена на комплексное число 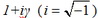 .
Это уравнение имеет очевидное решение .
Это уравнение имеет очевидное решение
Умножим числитель и знаменатель этой дроби на комплексно сопряженное к знаменателю число
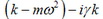 . .
Нетрудно видеть, что если заменить в этом решении величину
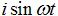 на на
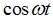 , то получиться в точности решение
предыдущей задачи со “сдвигом фаз”. , то получиться в точности решение
предыдущей задачи со “сдвигом фаз”.
Огромным преимуществом такого подхода является его простота. Достаточно вместо обычных математических
операций запрограммировать операции над комплексными числами и решение у нас “в кармане”. Еще одним
достоинством такого подхода является то, что он дает возможность дифференцированно учесть поглощение
энергии для разных элементов конструкции. Для этого достаточно при формировании матрицы жесткости конструкции,
внося реакции конкретного элемента в систему, умножить их на
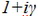 с коэффициентом
g, присущим материалу,
из которого изготовлен данный элемент. Практика показывает, что такой метод дает отличные результаты.
Недостатком данного подхода является то, что он применим только для гармонических возмущений. Для всех
других типов возмущения он дает неправильные результаты. с коэффициентом
g, присущим материалу,
из которого изготовлен данный элемент. Практика показывает, что такой метод дает отличные результаты.
Недостатком данного подхода является то, что он применим только для гармонических возмущений. Для всех
других типов возмущения он дает неправильные результаты.
|