|
3.18. Учет взаимодействия конструкции с подстилающим слоем грунта
Программа предусматривает несколько возможностей учета упругих свойств грунтового основания. Простейший вариант винклерового основания можно реализовать, используя конечные элементы одноточечной линейной упругой связи (тип элемента sp; см. Создание новых конечных элементов). Если необходимо учесть взаимодействие пластины с упругим основанием, поступите следующим образом:
|
|
| 1. |
Войдите в Графический редактор. |
| 2. |
Создайте треугольную или прямоугольную сетку. |
| 3. |
Присоедините к ней конечные элементы пластины (элементы t или rt). |
| 4. |
Войдите в режим ЭЛЕМЕНТЫ/  /СОЗДАТЬ. /СОЗДАТЬ.
|
| 5. |
Пометьте все узлы пластины и кликните по кнопке + Создать. |
6.
|
В выпадающем меню выберите Связи, нормальные к заданной
поверхности  . . |
7.
|
Выберите в левом верхнем меню Инструменты/Свойства и задайте для сгенерированной группы пружин коэффициент постели. |
|
Если упругие связи были созданы так, как было описано выше, то программа сама пересчитает жесткость каждой отдельной пружины, умножив коэффициент постели на площадь поверхности, прилегающей к каждой такой связи. Пусть вас не смущает, что в колонке Единицы измерения будет указана размерность [Сила]/[Длина] (размерность жесткости единичной связи). В данном конкретном случае размерность единиц будет [Сила]/[Длина]3.
Главным недостатком винклеровой модели основания является то, что она не учитывает распределительные свойства грунта. Альтернативой использования винклеровой модели основания является модель упругого полупространства или модель упругого слоя. В этом случае основание моделируется набором объемных конечных элементов (элементы td и pr), свойства которых зависят от глубины залегающего слоя. Очевидным недостатком такой модели является значительное увеличение размеров модели (количество переменных, идущих на описание основания, может значительно превышать число переменных самой конструкции).
В настоящее время разработано несколько механических моделей основания, с одной стороны позволяющих участь распределительные свойства грунта, а с другой – не требующих больших вычислительных затрат. Простейшей из таких моделей является модель основания с двумя коэффициентами постели (двухпараметровая модель). Физически такую модель можно представить следующим образом
На винклерово упругое основание с коэффициентом постели C1, наложена мембрана, края которой растягиваются постоянным усилием C2 (из расчета на единицу длины периметра). Размерность коэффициента C1 - [Сила]/[Длина]3, C2 - [Сила]/[Длина]. Очевидно, если в двухпараметровой модели положить C2= 0, то сразу получаем винклерову модель основания.
Для построения такой модели в программе предусмотрены 4 типа конечных элементов. Это два элемента пластин – треугольный элемент t и прямоугольный элемент rt и два элемента собственно упругого основания – треугольный элемент ft и прямоугольный элемент fr. Подключение к элементам пластин (элементы t и rt) упругого основания достигается тем, что наряду с толщиной пластины в ее свойствах можно дополнительно указать коэффициенты постели C1и C2. Если они не заданы (или равны 0), элементы обрабатываются как обычная пластина. Если хотя бы один из этих параметров отличен от нуля, элемент пластины рассматривается как элемент на упругом основании (см. Конечные элементы). Для элементов ft и fr в качестве параметров задаются коэффициенты C1и C2.
Чтобы правильно построить модель упругого основания, поступите следующим образом:
|
|
| 1. |
Постройте модель конструкции. |
2.
|
В Графическом редакторе в режиме СХЕМА перейдите в новый слой и нарисуйте очертания фундаментных плит и контур будущего грунтового основания (контур основания – это может быть или круг или прямоугольник, охватывающий с некоторым запасом точки крепления конструкции к “земле”).
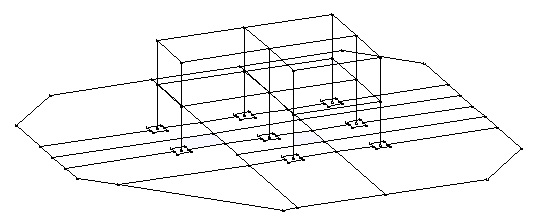
(дополнительные линии проведены с целью улучшить качество сетки). |
3.
|
Добавьте узлы крепления конструкции к фундаментным плитам к слою, в котором были нарисованы контуры основания - СХЕМА/СЛОИ/+ Добавить к слою (это облегчит вам процедуру генерации основания). |
4.
|
Закройте все слои, кроме того, в котором было нарисованы контуры основания, и сгенерируйте треугольную сетку – ГЕНЕР.ОБОЛ./  . При этом не забудьте узлам крепления конструкции к фундаментным плитам дать статус фиксированных узлов (ГЕНЕР.ОБОЛ./ . При этом не забудьте узлам крепления конструкции к фундаментным плитам дать статус фиксированных узлов (ГЕНЕР.ОБОЛ./  /ФИКС.УЗЛЫ). /ФИКС.УЗЛЫ).
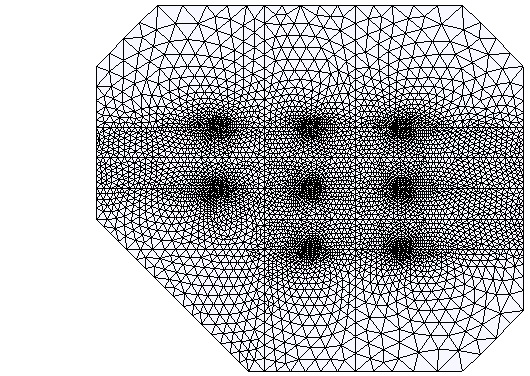 |
5.
|
Войдите в режим ЭЛЕМЕНТЫ и прикрепите к треугольной сетке, образующей фундаментные плиты треугольные элементы пластин (элементы t), а к сетке, образующей собственно грунтовое основание треугольные элементы упругого основания (элементы ft).
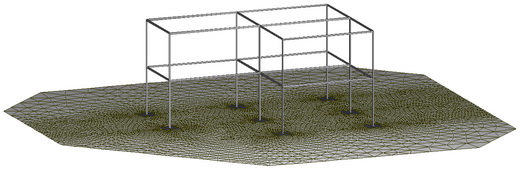 |
|
Свойства элементов задаются, как обычно, в окне свойств (Инструменты/Свойства). Окно Свойства содержит инструмент для вычисления коэффициентов постели C1 и C2. Если в списке групп жесткостей выбирается элемент пластины или элемент упругого основания, становится активной кнопка Основание.
Щелчок по этой кнопке открывает новое окно, позволяющее вычислить коэффициентов C1 и C2 в зависимости от свойств подстилающих грунтов
(более подробно см. Задание свойств конечных элементов).
Заметим, что будет грубой ошибкой крепление конструкции непосредственно к грунтовому основанию без использования переходной фундаментной плиты. Решение задачи о сосредоточенной силе, приложенной к двухпараметровому упругому основанию, имеет особенность в точке приложения силы и, поэтому, при уменьшении размеров конечных элементов будет вообще расходиться. Это же замечание касается и модели упругого слоя конечной толщины.
Заметим также, что в случае использования либо винклеровой либо двухпараметровой модели упругого основания, никаких дополнительных креплений (внешних связей) в вертикальном направлении на конструкцию накладывать не надо. Однако в нашем случае ничто не препятствует перемещаться конструкции вместе с основанием в горизонтальной плоскости. Поэтому на узлы крепления рамы к фундаментным плитам следует наложить связи, препятствующие смещению вдоль осей X и Y.
Общая картина деформации основания нашей конструкции будет иметь вид
Программа сама не вычисляет давление по подошве фундаментных плит. Однако эти напряжения могут быть вычислены без труда самим пользователем по простой формуле
где A, Ix, Iy – площадь и моменты инерции фундаментной плиты относительно осей x и y, a и b – размеры плиты вдоль осей x и y, N, Mx, My – вертикальная сила и моменты относительно соответствующих осей плиты, приложенные к ней. Использование для определения давления по подошве фундаментной плиты псевдоэлемента плиты основания (элемент bs, см. Конечные элементы), будет ошибкой, поскольку данный элемент всегда требует закрепления вертикальной степени свободы Z, что исключает взаимодействие с грунтом.
|
|
|