|
3.2.3. Определение расчетных длин балочных элементов
Как показано в разделе Проверка устойчивости стержневых конструкций, устойчивость стержневой конструкции может быть оценена на основе расчета конструкции с учетом начальных несовершенств. Наличие фибровых напряжений в сжатых элементах, превышающих предел текучести, является четким сигналом того, что конструкция может потерять устойчивость. Тем не менее, множество нормативных проверок отталкивается от понятия “расчетной длины” стержневого элемента. Стандартный подход к определению расчетных длин состоит из следующих этапов: делается статический расчет конструкции на заданную комбинацию загружений, полученные продольные усилия в стержнях Ni рассматривается как параметрическая нагрузка (параметрическая нагрузка, в отличие от внешней нагрузки, это внутренние усилия в конструкции, от которых зависит ее жесткость) и отыскивается такой множитель kкр к этим усилиям, чтобы после возникновения в стержнях усилий kкрNi конструкция теряла устойчивость. Расчетная длина i-го стержня определяется по формуле
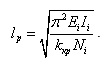
Недостатки такого подхода хорошо известны. Как правило, за общую потерю устойчивости отвечает некоторая ограниченная группа элементов и в первую очередь эти элементы влияют на значение коэффициента kкр. Поскольку этот коэффициент единый для всей системы, то применение его к слабо загруженным элементам приводит к чрезвычайно завышенным расчетным длинам. Кроме того, невозможно разделить гибкости элемента относительно его главных осей – по данной методике гибкости стержня относительно обеих осей получаются одинаковыми. Фактически традиционный подход позволяет более-менее оценить расчетные длины для очень ограниченной группы стержней, действительно ответственных за потерю устойчивости всей конструкции.
Физически расчетная длина стержня – это расстояние между парой соседних нулей на эпюре моментов стержня, подверженному продольному изгибу. Этим, считается, произвольный стержень как бы приводится к шарнирному с обоих концов стержню, для которого решение задачи продольного изгиба хорошо известно. Если принять, что выпучивание стержня при продольном изгибе происходит по форме потери устойчивости, то для того, чтобы определить это расстояние, достаточно знать геометрические характеристики стержня и реакции остальной части системы на тестируемый стержень в узлах его прикрепления к конструкции. Когда выполняется расчет конструкции на общую потерю устойчивости, фактически отыскивается критическая сила в каждом отдельно взятом стержне (т.е. сила, от которой он потеряет устойчивость), но при условии, что параллельно с изменением этого усилия пропорционально меняются усилия и во всех остальных элементах конструкции. Поскольку увеличение сжимающей силы в стержне в определенном смысле эквивалентно уменьшению его изгибной жесткости, это приводит к тому, что реакции со стороны отброшенной части конструкции на стержень уменьшаются и, соответственно снижается уровень критического усилия, необходимого для тог, чтобы тестируемый стержень потерял устойчивость. Дальше действует все та же формула для определения расчетной длины стержня - 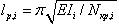 , вследствие чего расчетная длина стержня оказывается завышенной. , вследствие чего расчетная длина стержня оказывается завышенной.
Выход состоит в том, чтобы зафиксировать напряженное состояние во всех элементах системы, кроме тестируемого элемента. В результате правильно будет учтена жесткость отброшенной части конструкции, а значения критической силы в тестируемом элементе и его расчетная длина приобретут реальное значение. При этом исчезает проблема “огромных расчетных длин”. Расчетные длины могут быть вычислены независимо друг от друга для обеих главных осей сечения. Понятие “расчетная длина” совершенно естественным образом может быть распространено на ненагруженные, и даже растягиваемые элементы.
Именно такой подход реализует данный режим расчета. Полученные таким образом расчетные длины стержневых элементов будут всегда несколько меньше, чем расчетные длины, полученные из расчета общей устойчивости (см. п.Линейный расчет). Чтобы подстраховаться, можно ввести небольшой повышающий коэффициент 1.1-1.2 к расчетной комбинации загружений (расчетная комбинация запрашивается при запуске расчета). Но следует следить за тем, чтобы расчетная комбинация не оказалась закритической.
Ниже на рисунке показана расчетная схема 4-х-этажной 4-х-пролетной рамы. Все стержни одинакового сечения. Этажи и перекрытие загружены одной и той же распределенной нагрузкой.
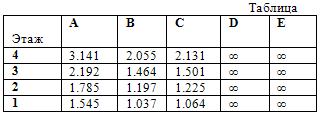
На графиках показаны рассчитанные кривые коэффициента свободной длины m для колонн (A,B,C) и ригелей (D,E). На этих графиках по шкале абсцисс откладывается уровень нагрузки по отношению к критическому состоянию. Цифрами обозначены номера этажей.
В таблице даны предельные значения коэффициента m, соответствующие критическому состоянию конструкции. Заметим, эти предельные значения как раз и соответствуют “стандартной” схеме расчета, кода при поиске критического состояния увеличение нагрузки происходит одновременно во всех элементах системы. Как следствие, в элементах ригелей, в которых изначально не было никаких усилий, получилось значение m=∞ (эффект огромных расчетных длин для слабо нагруженных элементов расчетчикам хорошо известен).
Ниже на рисунке изображена шпренгельная ферма, подкрепленная в а пяти точках верхнего пояса из своей плоскости. Верхний пояс составлен из двутавров СТО АС4М 20-93 16В2 (Jy=6.83•10-7, Jz=8.69•10-6). Нижний пояс – двутавр 12В2 (Jy=2.77•10-7, Jz=3.18•10-6). Раскосы и стойки – квадратный профиль 60х6. Шпренгельные связи – квадрат 50х5.5. К верхнему поясу приложена вертикальная распределенная нагрузка 15000 Н/м, что составляет 92% от критической нагрузки (потеря устойчивости происходит выпучиванием из плоскости фермы).
На рисунке (b) рядом с каждым элементом фермы показаны рассчитанные значения коэффициента свободной длины m: верхние значения соответствуют изгибу элементов из плоскости фермы, нижние – в плоскости фермы. На рисунке ниже даны значения коэффициента свободной длины для элементов той же фермы, рассчитанные на основе линейного расчета на устойчивость.
Стандартная методика позволяет вычислить расчетные длины только для сжатых элементов и только при изгибе относительно одной из главных осей стержня (в данном случае, при изгибе из плоскости фермы). Как видно, есть некоторое соответствие между значениями коэффициента my для элементов верхнего пояса между точками крепления опорных раскосов, рассчитанным по обеим методикам. Все остальные элементы слабо нагружены и для них программа выдает неприемлемые значения коэффициента m.
|